题目内容
设数列{an}是首项a1=1的等比数列，若{
}是等差数列，则(
+
）+(
+
）+…+(
+
）的值为 ．
| 1 |
| 2an+an+1 |
| 1 |
| 2a1 |
| 1 |
| a2 |
| 1 |
| 2a2 |
| 1 |
| a3 |
| 1 |
| 2a2012 |
| 1 |
| a2013 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由已知条件推导出2an+an+1=3，由此能求出（
+
）+（
+
）+…+（
+
）的值．
| 1 |
| 2a1 |
| 1 |
| a2 |
| 1 |
| 2a2 |
| 1 |
| a3 |
| 1 |
| 2a2012 |
| 1 |
| a2013 |
解答：
解：设等比数列{an}的公比为q，a1=1，
∴an=qn-1，
∴
=
，
∵{
}是等差数列，
∴2×
=
+
，
整理，得q2-2q+1=0，解得q=1，
∴an=1n-1=1，
∴2an+an+1=3，
∴（
+
）+（
+
）+…+（
+
）
=
=
×2012
=3018．
故答案为：3018．
∴an=qn-1，
∴
| 1 |
| 2an+an+1 |
| 1 |
| 2qn-1+qn |
∵{
| 1 |
| 2an+an+1 |
∴2×
| 1 |
| 2q2-1+q2 |
| 1 |
| 2q1-1+q |
| 1 |
| 2q3-1+q3 |
整理，得q2-2q+1=0，解得q=1，
∴an=1n-1=1，
∴2an+an+1=3，
∴（
| 1 |
| 2a1 |
| 1 |
| a2 |
| 1 |
| 2a2 |
| 1 |
| a3 |
| 1 |
| 2a2012 |
| 1 |
| a2013 |
=
| ||||||||||
| 2012个 |
=
| 3 |
| 2 |
=3018．
故答案为：3018．
点评：本题考查等差数列的前n项和的求法，是中档题，解题时要认真审题，注意等比数列的性质的灵活运用．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
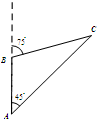一只艘船以均匀的速度由A点向正北方向航行，如图，开始航行时，从A点观测灯塔C的方位角（从正北方向顺时针转到目标方向的水平角）为45°，行驶60海里后，船在B点观测灯塔C的方位角为75°，则A到C的距离是