题目内容
已知直线l:x+y+m=0(m∈R)与圆C:x2+y2+2x+4y-4=0相交于A、B两点.
(1)若|AB|﹦2,求m的值;
(2)是否存在实数m,使得以AB为直径的圆经过原点O?若存在,请求出这样的m;若不存在,请说明理由.
(1)若|AB|﹦2,求m的值;
(2)是否存在实数m,使得以AB为直径的圆经过原点O?若存在,请求出这样的m;若不存在,请说明理由.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)圆的方程化为标准方程,求出圆心与半径,由|AB|﹦2,可得直线l:x+y+m=0过圆心,即可求出m的值;
(2)假设存在实数m,使得以线段AB为直径的圆经过坐标原点,则kOA•kOB=-1,即x1x2+y1y2=0,整理后代入根与系数关系求解实数m的值.
(2)假设存在实数m,使得以线段AB为直径的圆经过坐标原点,则kOA•kOB=-1,即x1x2+y1y2=0,整理后代入根与系数关系求解实数m的值.
解答:
解:(1)圆C:x2+y2+2x+4y-4=0可化为:(x+1)2+(y+2)2=1,
∴圆心C(-1,-2),半径为1,
∵|AB|﹦2,
∴直线l:x+y+m=0过圆心,
∴-1-2+m=0,
∴m=3;
(2)记A(x1,y1),B(x2,y2),
假设存在实数m,使得以线段AB为直径的圆经过坐标原点,
则kOA•kOB=-1,即x1x2+y1y2=0,
∴x1x2+(-x1-m)(-x2-m)=0,
即2x1x2+m(x1+x2)+m2=0,
直线l:x+y+m=0(m∈R)与圆C:x2+y2+2x+4y-4=0联立,消去y,
可得2x2+(2m-2)x+m2-4m-4=0,
∴x1+x2=1-m,2x1x2=m2-4m-4,
∴m2-4m-4+m(1-m)+m2=0,
∴m2-3m-4=0,
∴m=-1或m=4,满足题意.
∴圆心C(-1,-2),半径为1,
∵|AB|﹦2,
∴直线l:x+y+m=0过圆心,
∴-1-2+m=0,
∴m=3;
(2)记A(x1,y1),B(x2,y2),
假设存在实数m,使得以线段AB为直径的圆经过坐标原点,
则kOA•kOB=-1,即x1x2+y1y2=0,
∴x1x2+(-x1-m)(-x2-m)=0,
即2x1x2+m(x1+x2)+m2=0,
直线l:x+y+m=0(m∈R)与圆C:x2+y2+2x+4y-4=0联立,消去y,
可得2x2+(2m-2)x+m2-4m-4=0,
∴x1+x2=1-m,2x1x2=m2-4m-4,
∴m2-4m-4+m(1-m)+m2=0,
∴m2-3m-4=0,
∴m=-1或m=4,满足题意.
点评:本题主要考查了直线与圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
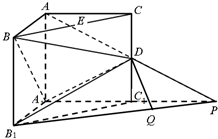 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.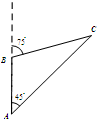 一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是
一只艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是