题目内容
已知函数g(x)=2x+
(1)求函数g(x)在[4,8]上的值域;
(2)求函数g(x)在(-2,0)∪(0,3)上的值域.
| 8 |
| x |
(1)求函数g(x)在[4,8]上的值域;
(2)求函数g(x)在(-2,0)∪(0,3)上的值域.
考点:函数的值域
专题:函数的性质及应用
分析:(1)利用函数在区间[4,8]上单调递增,求出函数的值域;
(2)利用双勾函数的单调性求出函数的值域.
(2)利用双勾函数的单调性求出函数的值域.
解答:
解:g(x)=2x+
的单调递增区间为(-∞,-2]和[2,+∞),单调递减区间为(-2,0)和(0,2);
(1)函数g(x)=2x+
在[4,8]上的单调递增,又g(4)=10,g(8)=17,
∴g(x)的值域为[10,17].
(2)函数g(x)=2x+
的在(-2,0)和(0,2)上单调递减,在(2,3)上单调递增,
又g(-2)=-8,g(2)=8,当x从负的趋向0时,g(x)趋向-∞,当x从正的趋向0时,g(x)趋向+∞,
∴g(x)的值域为(-∞,-8)∪[8,+∞).
| 8 |
| x |
(1)函数g(x)=2x+
| 8 |
| x |
∴g(x)的值域为[10,17].
(2)函数g(x)=2x+
| 8 |
| x |
又g(-2)=-8,g(2)=8,当x从负的趋向0时,g(x)趋向-∞,当x从正的趋向0时,g(x)趋向+∞,
∴g(x)的值域为(-∞,-8)∪[8,+∞).
点评:双勾函数的单调区间同学们应该熟记,撑握了它的性质,解决这题应该不是难事.属于基础题.

练习册系列答案
相关题目
已知x,y满足x≥0,x2+(y-2)2=2,则w=
的最大值为( )
| 3x2+2xy+3y2 |
| x2+y2 |
| A、4 | B、5 | C、6 | D、7 |
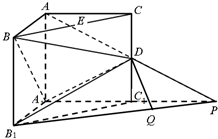 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面A1B1C1,∠BAC=90°,AB=AC=AA1=1,D是棱CC1的中点,P是AD的延长线与A1C1的延长线的交点.