题目内容
2.已知奇函数f(x)的定义域为[-2,2],且在定义域上单调递减,则满足不等式f(1-m)+f(1-2m)<0的实数m的取值范围是[-$\frac{1}{2}$,$\frac{2}{3}$].分析 根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:∵函数奇函数f(x)的定义域为[-2,2],且在定义域上单调递减,
∴不等式f(1-m)+f(1-2m)<0等价为f(1-m)<-f(1-2m)=f(2m-1),
即$\left\{\begin{array}{l}{-2≤1-m≤2}\\{-2≤2m-1≤2}\\{1-m≥2m-1}\end{array}\right.$,即$\left\{\begin{array}{l}{-1≤m≤3}\\{-\frac{1}{2}≤m≤\frac{3}{2}}\\{m≤\frac{2}{3}}\end{array}\right.$,得-$\frac{1}{2}$≤m≤$\frac{2}{3}$,
故答案为:[-$\frac{1}{2}$,$\frac{2}{3}$]
点评 本题主要考查不等式的求解,根据函数奇偶性将不等式进行转化是解决本题的关键.注意定义域的限制.

练习册系列答案
相关题目
7.已知定义在R上的奇函数f (x)满足f(x)=f(4-x),且在区间[0,2]上是增函数,那么( )
| A. | f(6)<f(4)<f(1) | B. | f(4)<f(6)<f(1) | C. | f(1)<f(6)<f(4) | D. | f(6)<f(1)<f(4) |
12.下列函数中,既是奇函数又在区间(0,+∞)上为增函数的是( )
| A. | y=lnx | B. | y=x3 | C. | y=x2 | D. | y=sinx |
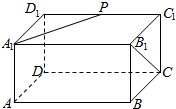 如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.
如图,在长方体ABCD-A1B1C1D1中,设 AD=AA1=1,AB=2,P是C1D1的中点,则$\overrightarrow{{B_1}C}与\overrightarrow{{A_1}P}$所成角的大小为60°,$\overrightarrow{{B_1}C}•\overrightarrow{{A_1}P}$=1.