过点且倾斜角为60°的直线方程为( )A．$\sqrt{3}x-y-2\sqrt{3}$-1=0B．$\sqrt{3}x-3y-2\sqrt{3}$-3=0C．$\sqrt{3}x-y+2\sqrt{3}$+1=0D．$\sqrt{3}x-3y+2\sqrt{3}+3=0$ 题目和参考答案——青夏教育精英家教网—

题目内容

12．过点（2，-1）且倾斜角为60°的直线方程为（　　）

A．

$\sqrt{3}x-y-2\sqrt{3}$-1=0

B．

$\sqrt{3}x-3y-2\sqrt{3}$-3=0

C．

$\sqrt{3}x-y+2\sqrt{3}$+1=0

D．

$\sqrt{3}x-3y+2\sqrt{3}+3=0$

分析由直线的倾斜角求出直线的斜率，代入直线方程的点斜式，整理为一般式得答案．

解答解：∵直线的倾斜角为60°，
∴斜率k=tan60°=$\sqrt{3}$，
又直线过点（2，-1），
由直线方程的点斜式得：y+1=$\sqrt{3}（x-2）$，
化为一般式：$\sqrt{3}x-y-2\sqrt{3}-1=0$．
故选：A．

点评本题考查直线的点斜式方程，考查了直线的倾斜角与斜率的关系，是基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

17．已知x^3k=5，y^2k=3，求x^6k•y^4k的值．

3．某校从2名男生和3名女生中随机选出3名学生做义工，则选出的学生中男女生都有的概率为$\frac{9}{10}$．

20．

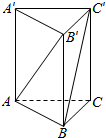如图，在正三棱柱ABC-A′B′C′中，若AA′=2AB，则异面直线AB′与BC′所成角的余弦值为（　　）

7．已知定义在R上的奇函数f （x）满足f（x）=f（4-x），且在区间[0，2]上是增函数，那么（　　）

17．抛物线y²=2px（p＞0）与直线y=x+1相切，A（x₁，y₁），B（x₂，y₂）（x₁≠x₂）是抛物线上两个动点，F为抛物线的焦点，且|AF|+|BF|=8．
（Ⅰ）求p的值；
（Ⅱ）线段AB的垂直平分线l与x轴的交点是否为定点，若是，求出交点坐标，若不是，说明理由；
（Ⅲ）求直线l的斜率的取值范围．

4．定义在（0，+∞）上的函数f（x），如果对任意x∈（0，+∞），都有f（kx）=kf（x）（k≥2，k∈N^*）成立，则称f（x）为k阶伸缩函数．
（Ⅰ）若函数f（x）为二阶伸缩函数，且当x∈（1，2]时，$f（x）=1+{log_{\frac{1}{3}}}x$，求$f（2\sqrt{3}）$的值；
（Ⅱ）若函数f（x）为三阶伸缩函数，且当x∈（1，3]时，$f（x）=\sqrt{3x-{x^2}}$，求证：函数$y=f（x）-\sqrt{2}x$在（1，+∞）上无零点；
（Ⅲ）若函数f（x）为k阶伸缩函数，且当x∈（1，k]时，f（x）的取值范围是[0，1），求f（x）在（0，kⁿ⁺¹]（n∈N^*）上的取值范围．

1．气象台预报“本市明天降雨概率是70%”，下列说法正确的是（　　）

	A．	本市明天将有70%的地区降雨		B．	本市明天将有70%的时间降雨
	C．	明天出行带雨具的可能性很大		D．	明天出行不带雨具肯定要淋雨

2．已知点$（a，\frac{1}{2}）$在幂函数f（x）=（a-1）x^b的图象上，则函数f（x）是（　　）

	A．	奇函数		B．	偶函数
	C．	定义域内的减函数		D．	定义域内的增函数

试题分类