题目内容
△ABC的三边a，b，c所对角分别是A，B，C，若a=
，c=1，S△ABC=
，则cosB= ．
| 3 |
| ||
| 4 |
考点：余弦定理,正弦定理
专题：解三角形
分析：利用三角形面积公式列出关系式，把a，c以及已知面积代入求出sinB的值，即可确定出cosB的值．
解答：
解：∵△ABC中，a=
，c=1，S△ABC=
，
∴
acsinB=
×
×1×sinB=
，
∴sinB=
，
则cosB=±
=±
．
故答案为：±
| 3 |
| ||
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
∴sinB=
| 1 |
| 2 |
则cosB=±
| 1-sin2B |
| ||
| 2 |
故答案为：±
| ||
| 2 |
点评：此题考查了余弦定理，三角形面积公式，熟练掌握定理是解本题的关键．
练习册系列答案
学习实践园地系列答案
相关题目
下列函数中，在其定义域内，既是奇函数又是减函数的是（ ）
A、f（x）=
| ||
B、f（x）=
| ||
| C、f（x）=-x3 | ||
| D、f（x）=2x-2-x |
若两个等差数列{an}，{bn}的前n项的和为An，Bn．且
=
，则
=（ ）
| An |
| Bn |
| 4n+5 |
| 5n-5 |
| a5+a13 |
| b5+b13 |
A、
| ||
B、
| ||
C、
| ||
D、
|
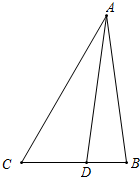如图，在△ABC中，已知4sin2