题目内容
16．曲线y=2x2-x在点（0，0）处的切线方程为（ ）| A． | x+y=0 | B． | x-y=0 | C． | x-y+2=0 | D． | x+y+2=0 |
分析 欲求曲线y=2x2-x在点（0，0）处的切线方程，只须求出其斜率即可，故先利用导数求出在x=0处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．
解答 解：∵y=f（x）=2x2-x，
∴f'（x）=4x-1，当x=0时，f'（0）=-1得切线的斜率为-1，所以k=-1；
所以曲线在点（0，0）处的切线方程为：
y-0=-（x-0），即x+y=0．
故选A．
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识，考查运算求解能力．属于基础题．
练习册系列答案
相关题目
7．将函数f（x）=cos2ωx的图象向右平移$\frac{3π}{4ω}$个单位，得到函数y=g（x）的图象，若y=g（x）在$[-\frac{π}{4}，\frac{π}{6}]$上为减函数，则正实数ω的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 3 |
4．已知集合A={0，2，4，6}，B={x∈N|2x＜33}，则集合A∩B的子集个数为（ ）
| A． | 8 | B． | 7 | C． | 6 | D． | 4 |
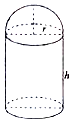某化工厂拟建一个下部为圆柱，上部为半球的容器（如图，圆柱高为h，半径为r，不计厚度，单位：米），按计划容积为72π立方米，且h≥2r，假设其建造费用仅与表面积有关（圆柱底部不计），已知圆柱部分每平方米的费用为2千元，半球部分每平方米4千元，设该容器的建造费用为y千元．
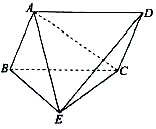如图四棱锥E-ABCD中，四边形ABCD为平行四边形，△BCE为等边三角形，△ABE是以∠A为直角的等腰直角三角形，且AC=BC．