题目内容
设函数f（x）=|x-1|-2，则f[f（5）]= ．
考点：函数的值
专题：函数的性质及应用
分析：根据所给的函数式，代入自变量5，求出函数的值，再把值代入函数的解析式，求出对应的函数的值．
解答：
解：∵f（x）=|x-1|-2，
∴f（5）=|5-1|-2=2，
∴f[f（5）]=f（2）=|2-1|-2=-1
故答案为：-1
∴f（5）=|5-1|-2=2，
∴f[f（5）]=f（2）=|2-1|-2=-1
故答案为：-1
点评：本题考查函数的值，两次应用函数的解析式求出函数的值，本题是一个简单的运算题目，注意数字的运算．
练习册系列答案
相关题目
直线l1，l2的斜率分别为-
，-
，若l1⊥l2，则实数a的值是（ ）
| 1 |
| a |
| 2 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知函数f（x）=ax3+bx+1（a，b∈R），f（lg（log3e））=2，则f（lg（ln3））=（ ）
| A、-2 | B、0 | C、1 | D、2 |
如图，空间四边形ABCD中，P、Q、R分别是AB、AD、CD的中点，平面PQR交BC于点S．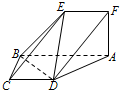
设平面ABCD⊥平面ABEF，AB∥CD，AB∥EF，∠BAF=∠ABC=90°，BC=CD=AF=EF=1，AB=2．