题目内容
函数y=2sin（2x+
）的单调递减区间为 ．
| π |
| 4 |
考点：正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：令2kπ+
≤2x+
≤2kπ+
，即可可解得函数y=2sin（2x+
）的单调递减区间．
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
解答：
解：令2kπ+
≤2x+
≤2kπ+
，可解得kπ+
≤x≤kπ+
，k∈Z．
所以函数y=2sin（2x+
）的单调递减区间为[kπ+
，kπ+
]，k∈Z．
故答案为：[kπ+
，kπ+
]，k∈Z．
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
所以函数y=2sin（2x+
| π |
| 4 |
| π |
| 8 |
| 5π |
| 8 |
故答案为：[kπ+
| π |
| 8 |
| 5π |
| 8 |
点评：本题主要考查了三角函数的图象与性质，正弦函数的单调性，属于基本知识的考查．
练习册系列答案
相关题目
已知两定点F1（-1，0）、F2（1，0），则命题甲：|F1F2|是|PF1|与|PF2|的等差中项，命题乙：动点P的轨迹是椭圆，则甲是乙的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
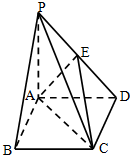如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点．