题目内容
8.三棱锥A-BCD中,AD⊥平面BCD,AD=1,△BCD是边长为2的等边三角形,则该几何体外接球的表面积为( )| A. | $\frac{17}{6}π$ | B. | $\frac{19}{6}π$ | C. | $\frac{17}{3}π$ | D. | $\frac{19}{3}π$ |
分析 由已知结合三棱锥和正三棱柱的几何特征,可得此三棱锥外接球,即为以△BCD为底面以DA为高的正三棱柱的外接球,分别求出棱锥底面半径r,和球心距d,可得球的半径R,即可求出三棱锥A-BCD外接球的表面积.
解答 解:根据已知中底面△BCD是边长为2的正三角形,DA⊥平面BCD,
可得此三棱锥外接球,即为以△BCD为底面以DA为高的正三棱柱的外接球
∵△BCD是边长为2的正三角形,
∴△BCD的外接圆半径r=$\frac{2}{\sqrt{3}}$,
球心到△BCD的外接圆圆心的距离d=$\frac{1}{2}$,R=$\sqrt{\frac{4}{3}+\frac{1}{4}}=\sqrt{\frac{19}{12}}$,
故三棱锥A-BCD外接球的表面积S=4πR2=$\frac{19π}{3}$.
故选:D
点评 本题考查的知识点是球内接多面体,正确求出球的半径R是解答的关键.属于中档题,

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.函数f(x)=x3+x2+5ax-1存在极值点的充要条件是( )
| A. | a$≤\frac{1}{15}$ | B. | a<$\frac{1}{15}$ | C. | a$≥\frac{1}{15}$ | D. | a>$\frac{1}{15}$ |
16.要得到函数$y=\frac{1}{2}cos2x$的图象,只需将函数$y=\frac{1}{2}sin2x$的图象( )
| A. | 向右平移$\frac{π}{2}$个单位 | B. | 向右平移$\frac{π}{4}$个单位 | ||
| C. | 向左平移$\frac{π}{2}$个单位 | D. | 向左平移$\frac{π}{4}$个单位 |
3.在下列区间中,函数f(x)=e-x+4x-3的零点所在的区间为( )
| A. | (-$\frac{1}{4}$,0) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
13.已知偶函数f(x)是定义在R上的可导函数,其导函数为f′(x),当x<0时有2f(x)+xf′(x)>x2,则不等式(x+2017)2f(x+2017)-f(-1)<0的解集为( )
| A. | (-∞,-2016) | B. | (-2018,-2016) | ||
| C. | (-2018,+∞) | D. | (-∞,-2018)∪(-2016,+∞) |
20.在区间[-3,3]上随机选取一个实数x,则事件“2x-3<0”发生的概率是( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
18.某几何体的三视图如图,则该几何体的体积为( )
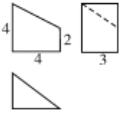

| A. | 18 | B. | 20 | C. | 24 | D. | 12 |