题目内容

10．设F1、F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，过点F2的直线交双曲线右支于A、B两点．若AF2⊥AF1，且|BF2|=2|AF1|，则双曲线的离心率为（　　）
A．$\frac{\sqrt{17}}{3}$B．$\frac{\sqrt{10}}{2}$C．$\sqrt{13}$D．$\frac{\sqrt{58}}{4}$

分析 由题意，设|AF2|=m，则|BF2|=2m，利用勾股定理，求出a，m的关系，再利用勾股定理确定a，c的关系，即可求出双曲线的离心率．

解答 解：由题意，设|AF2|=m，则|BF2|=2m，
∴|AF1|=2a+m，|BF1|=2a+2m，
∵AF2⊥AF1，
∴（2a+2m）2=（2a+m）2+（3m）2，
∴m=$\frac{2}{3}$a，
∵（2c）2=（2a+m）2+（m）2，
∴e=$\frac{c}{a}$=$\frac{\sqrt{17}}{3}$．
故选A．

点评 本题考查双曲线的离心率，考查勾股定理的运用，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
20．设函数f（x）=|x-1|+$\frac{1}{2}$|x-3|．
（1）作出函数图象，并求不等式f（x）＞2的解集；
（2）设g（x）=$\frac{{x}^{2}+m}{x}$，若对于任意的x1，x2∈[3，5]都有f（x1）≤g（x2）恒成立，求正实数m的取值范围．
1．设椭圆C$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左右焦点分别为F1，F2，l是右准线，若椭圆上存在一点P使得PF1是P到直线l的距离的3倍，则椭圆的离心率的取值范围是[$\sqrt{7}$-2，1）．
18．已知数列{an}满足：${a_1}=1，{a_2}=2，{a_{n+2}}={a_{n+1}}-{a_n}（n∈{N^*}）$，函数f（x）=ax3+btanx，若f（a4）=9，则f（a1）+f（a2017）的值是-18．
5．在直角坐标标系xoy中，已知曲线${C_1}：\left\{{\begin{array}{l}{x=1+cosα}\\{y={{sin}^2}α-\frac{9}{4}}\end{array}}\right.$（α为参数，α∈R），在以原点O为极点，x轴非负半轴为极轴的极坐标系中（取相同的长度单位），曲线${C_2}：ρsin（θ+\frac{π}{4}）$=$-\frac{{\sqrt{2}}}{2}$，曲线C3：ρ=2cosθ．
（Ⅰ）求曲线C1与C2的交点M的直角坐标；
（Ⅱ）设A，B分别为曲线C2，C3上的动点，求|AB|的最小值．
15．若?x∈（-1，2），ax+2≠0是假命题的一个充分不必要条件为a∈（　　）
A．（-∞，-1）∪（2，+∞）B．（-1，2）C．（-∞，-1）D．（-∞，-1]∪[2，+∞）
2．已知不等式$\frac{{{2^x}+1}}{3}＞1-\frac{{{2^x}-1}}{2}$的解集为M，则下列说法正确的是（　　）
A．{0}⊆MB．M=∅C．-1∈MD．2∈M
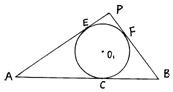19．如图，△PAB的顶点A、B为定点，P为动点，其内切圆O1与AB、PA、PB分别相切于点C、E、F，且$AB=2\sqrt{3}$，||AC|-|BC||=2．
（1）求||PA|-|PB||的值；
（2）建立适当的平面直角坐标系，求动点P的轨迹W的方程；
（3）设l是既不与AB平行也不与AB垂直的直线，线段AB的中点O到直线l的距离为 $\sqrt{2}$，直线l与曲线W相交于不同的两点G、H，点M满足$2\overrightarrow{OM}=\overrightarrow{OG}+\overrightarrow{OH}$，证明：$2|\overrightarrow{OM}|=|\overrightarrow{GH}|$．
20．已知某几何体的三视图如图所示，其中俯视图中的曲线是一段半圆弧，则这个几何体的表面积是12+π．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网