题目内容
11.已知命题p:?x0∈R,lnx0≥x0-1.命题q:?θ∈R,sinθ+cosθ>-1.则下列命题中为真命题的是( )| A. | p∧(?q) | B. | (?p)∨q | C. | (?p)∧(?q) | D. | p∧q |
分析 先判断命题p和命题q的真假,进而根据复合命题真假判断的真值表,得到答案.
解答 解::?x0=1∈R,使lnx0=x0-1=0.
故命题p:?x0∈R,lnx0≥x0-1为真命题,
当θ∈[π+2kπ,$\frac{3π}{2}$+2kπ]时,sinθ+cosθ∈[$-\sqrt{2}$,-1],
故命题q:?θ∈R,sinθ+cosθ>-1为假命题,
故命题p∧(?q)为真命题,
命题(?p)∨q,(?p)∧(?q),p∧q为假命题,
故选:A
点评 本题以命题的真假判断与应用为载体,考查了复合命题,全称命题和特称命题等知识点,难度中档.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
2.已知不等式$\frac{{{2^x}+1}}{3}>1-\frac{{{2^x}-1}}{2}$的解集为M,则下列说法正确的是( )
| A. | {0}⊆M | B. | M=∅ | C. | -1∈M | D. | 2∈M |
6.函数$y=\sqrt{{{log}_2}(x-3)}$的定义域是( )
| A. | (3,+∞) | B. | (3,4] | C. | (4,+∞) | D. | [4,+∞) |
3.设F1,F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{25}=1(a<5)$的两个焦点,且|F1F2|=8,弦AB过点F2,则△ABF1的周长为( )
| A. | 12 | B. | 20 | C. | 2$\sqrt{41}$ | D. | 4$\sqrt{41}$ |
1.若函数f(x)满足f(3x+2)=9x+8,则f(x)的解析式是( )
| A. | f(x)=9x+8 | B. | f(x)=3x+2 | ||
| C. | f(x)=-3x-4 | D. | f(x)=3x+2或f(x)=-3x-4 |
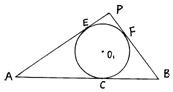 如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.
如图,△PAB的顶点A、B为定点,P为动点,其内切圆O1与AB、PA、PB分别相切于点C、E、F,且$AB=2\sqrt{3}$,||AC|-|BC||=2.