题目内容
6.已知三棱锥A-BCD的所有棱长都相等,若AB与平面α所成角等于$\frac{π}{3}$,则平面ACD与平面α所成角的正弦值的取值范围是( )| A. | [$\frac{3-\sqrt{6}}{6}$,$\frac{3+\sqrt{6}}{6}$] | B. | [$\frac{3-\sqrt{6}}{6}$,1] | C. | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$,$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{6}$] | D. | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$,1] |
分析 由题意求出AB与平面ACD所成角的正弦值和余弦值,然后分类求出平面ACD与平面α所成角的正弦值的最小值与最大值得答案.
解答 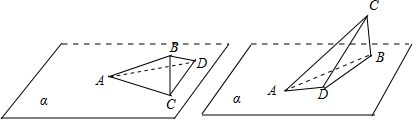 解:∵三棱锥A-BCD的所有棱长都相等,
解:∵三棱锥A-BCD的所有棱长都相等,
∴三棱锥A-BCD为正四面体,如图: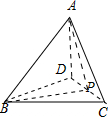
设正四面体的棱长为2,取CD中点P,连接AP,BP,
则∠BAP为AB与平面ADC所成角.
AP=BP=$\sqrt{3}$,可得sin$∠BAP=\frac{\sqrt{6}}{3}$,cos∠BAP=$\frac{\sqrt{3}}{3}$.
设∠BAP=θ.
当CD与α平行且AB在面ACD外时,平面ACD与平面α所成角的正弦值最小,
为sin($\frac{π}{3}-θ$)=sin$\frac{π}{3}cosθ$$-cos\frac{π}{3}sinθ$=$\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{3}-\frac{1}{2}×\frac{\sqrt{6}}{3}=\frac{3-\sqrt{6}}{6}$;
当CD与α平行且AB在面ACD内时,平面ACD与平面α所成角的正弦值最大,
为sin($\frac{π}{3}+θ$)=sin$\frac{π}{3}cosθ+$cos$\frac{π}{3}sinθ$=$\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{3}+\frac{1}{2}×\frac{\sqrt{6}}{3}=\frac{3+\sqrt{6}}{6}$.
∴平面ACD与平面α所成角的正弦值的取值范围是[$\frac{3-\sqrt{6}}{6}$,$\frac{3+\sqrt{6}}{6}$].
故选:A.
点评 本题考查二面角的平面角及其求法,考查数形结合的解题思想方法,考查空间想象能力和思维能力,是中档题.

| A. | 如果不买彩票,那么就不能中奖,因为你买了彩票,所以你一定中奖 | |
| B. | 因为a>b,a>c,所以a-b>a-c | |
| C. | 若a,b均为正实数,则lg a+lg b≥$\sqrt{lga•lgb}$ | |
| D. | 若a为正实数,ab<0,则$\frac{a}{b}$+$\frac{b}{a}$=-($\frac{-a}{b}$+$\frac{-b}{a}$)≤-2 $\sqrt{(\frac{-a}{b})•(\frac{-b}{a})}$=-2 |
 阅读下列伪代码,当a,b的输入值分别为2,3时,则输出的实数m的值是3.
阅读下列伪代码,当a,b的输入值分别为2,3时,则输出的实数m的值是3.