题目内容
15．解不等式：x2＞（k+1）x-k．分析 首先对不等式变形，然后分解因式，讨论对应根k与1的大小，得到不等式的解集．
解答 解：x2＞（k+1）x-k变形为（x-k）（x-1）＞0，
所以当k＞1时，不等式的解集是{x|x＜1或x＞k}；
当k=1时，不等式的解集是{x|x≠1}
当k＜1时，不等式的解集是{x|x＜k或x＞1}．
点评 本题考查了含有参数的一元二次不等式的解法；考查了讨论的思想．
练习册系列答案
相关题目
6．已知三棱锥A-BCD的所有棱长都相等，若AB与平面α所成角等于$\frac{π}{3}$，则平面ACD与平面α所成角的正弦值的取值范围是（ ）
| A． | [$\frac{3-\sqrt{6}}{6}$，$\frac{3+\sqrt{6}}{6}$] | B． | [$\frac{3-\sqrt{6}}{6}$，1] | C． | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$，$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{6}$] | D． | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$，1] |
某公路段在某一时刻内监测到的车速频率分布直方图如图所示．
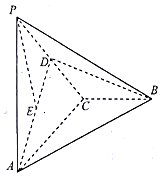如图，在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，D为PC的中点，E为AD的中点，PA=AC=2，BC=1．
在斜三棱柱ABC-A1B1C1中，顶点A1在底面ABC内的射影恰为线段AB的中点，AA1=2，△ABC为边长为2的正三角形，N为△ABC的中心，$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$．