题目内容
在等比数列{an}中,a2-a1=2,且2a2为3a1和a3的等差中项.
(1)求数列的{an}的通项公式;
(2)设Sn为数列an的前n项和,求Sn.
(1)求数列的{an}的通项公式;
(2)设Sn为数列an的前n项和,求Sn.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)利用等比数列与等差数列的通项公式即可得出.
(2)利用等比数列的前n项和公式即可得出.
(2)利用等比数列的前n项和公式即可得出.
解答:
解:(1)设等比数列{an}的公比为q,
∵a2-a1=2,且2a2为3a1和a3的等差中项.
∴a1q-a1=2,4a2=3a1+a3,即4a1q=3a1+a1q2,化为4q=3+q2,
解得a1=1,q=3.
∴an=3n-1.
(2)Sn=
=
(3n-1).
∵a2-a1=2,且2a2为3a1和a3的等差中项.
∴a1q-a1=2,4a2=3a1+a3,即4a1q=3a1+a1q2,化为4q=3+q2,
解得a1=1,q=3.
∴an=3n-1.
(2)Sn=
| 3n-1 |
| 3-1 |
| 1 |
| 2 |
点评:本题考查了等比数列与等差数列的图象四个及其前n项和公式即,考查了计算能力,属于基础题.

练习册系列答案
相关题目
已知向量
,
满足|
|=1,|
|=4且
•
=-2,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、150° | B、120° |
| C、60° | D、30° |
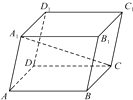 如图所示,在平行六面体ABCD-A1B1C1D1中,若
如图所示,在平行六面体ABCD-A1B1C1D1中,若| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| A1C |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、
|




