题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{{e}^{f(|x|+1)},x<1}\end{array}\right.$,(e为自然对数的底数),则f(e)=1,函数y=f(f(x))-1的零点有3个.(用数字作答)分析 化简f(x)的解析式,求出f(x)=1的解x0,再令f(x)=x0即可得出函数的零点.
解答 解:f(e)=lne=1,
f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{x+1,0≤x<1}\\{1-x,x<0}\end{array}\right.$,令f(x)=1得x=e或x=0,
∵f(f(x))-1=0,
∴f(x)=e或f(x)=0,
x=ee或x=1-e或x=1,
故y=f(f(x))-1有三个零点.
故答案为:1,3.
点评 本题考查了函数零点的个数判断,对数的运算性质,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
8.下列说法正确的是( )
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
9. 如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1.
 如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.(1)求证:B1C1∥平面BCD1;
(2)求证:平面A1ABB1⊥平面BCD1.
3.设集合A={3,log2(a-2)},B={a,a+b},若A∩B={1},则b的值为( )
| A. | -3 | B. | 3 | C. | 1 | D. | -1 |
10.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x≤0}\\{{e}^{x},x>0}\end{array}\right.$,则满足f(f(m))>f(m)+1的m的取值范围是( )
| A. | $({-\frac{1}{2},+∞})$ | B. | )(0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
7.函数f(x)=(cosx)•ln|x|的大致图象是( )
| A. |  | B. |  | ||
| C. |  | D. | 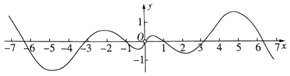 |
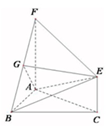 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.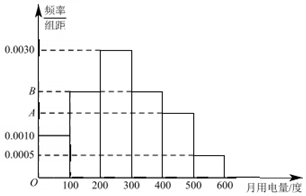 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.