题目内容

7．函数f（x）=（cosx）•ln|x|的大致图象是（　　）
A．B．
C．D．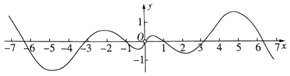

分析 判断函数的奇偶性排除选项，然后利用特殊点的位置判断即可．

解答 解：函数f（x）=（cosx）•ln|x|是偶函数，排除C，D．
当x=$\frac{π}{6}$时，f（$\frac{π}{6}$）=$\frac{\sqrt{3}}{2}$•ln$\frac{π}{6}$＜0．
排除A，
故选：B．

点评 本题考查函数的图象的判断，函数的奇偶性以及函数的特殊点的位置的应用，考查计算能力．

练习册系列答案
相关题目
17．如图所示，等腰梯形ABCD的底角A等于60°．直角梯形ADEF所在的平面垂直于平面
ABCD，∠EDA=90°，且ED=AD=2AF=2AB=2．
（Ⅰ）证明：平面ABE⊥平面EBD；
（Ⅱ）点M在线段EF上，试确定点M的位置，使平面MAB与平面ECD所成的角的余弦值为$\frac{\sqrt{3}}{4}$．
18．已知函数f（x）=$\left\{\begin{array}{l}{lnx，x≥1}\\{{e}^{f（|x|+1）}，x＜1}\end{array}\right.$，（e为自然对数的底数），则f（e）=1，函数y=f（f（x））-1的零点有3个．（用数字作答）
15．设{an}是单调递增的等差数列，Sn为其前n项和，且满足3S4=2S5，a5+2是a3，a12的等比中项．
（I）求数列{an}的通项公式；
（II）若数列{bn}满足$\frac{b_1}{a_1}+\frac{b_2}{a_2}+…+\frac{b_n}{a_n}={3^{n+1}}-3（{n∈{N^*}}）$，求数列{bn}的前n项和Tn．
2．若复数z1，z2在复平面内对应的点关于x轴对称，且z1=1+2i，则$\frac{z_1}{z_2}$=（　　）
A．$-\frac{4}{5}+\frac{3}{5}i$B．$-\frac{3}{5}+\frac{4}{5}i$C．$-\frac{1}{2}+\frac{3}{2}i$D．$-\frac{1}{2}-\frac{3}{2}i$
12．若复数z满足iz=1+i，则z的共轭复数$\overline{z}$在复平面内所对应点的坐标为（　　）
A．（1，1）B．（1，-1）C．（-1，1）D．（-1，-1）
19．函数f（x）=sin（2x+φ）（|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{6}$个单位后关于y轴对称，则f（x）在[0，$\frac{π}{2}$]上的单调递增区间为[$\frac{5π}{12}$，$\frac{π}{2}$]．
16．已知向量$\overrightarrow a，\overrightarrow b$的夹角为$\frac{5π}{6}，|{\overrightarrow a}|=2，|{\overrightarrow b}|=\sqrt{3}$，则$\overrightarrow a•（{2\overrightarrow b-\overrightarrow a}）$=-10．
15．已知椭圆$C：\frac{x^2}{6}+\frac{y^2}{2}=1$，点A（3，0），P是椭圆C上的动点．
（I）若直线AP与椭圆C相切，求点P的坐标；
（II）若P在y轴的右侧，以AP为底边的等腰△ABP的顶点B在y轴上，求四边形OPAB面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网