题目内容
3.设集合A={3,log2(a-2)},B={a,a+b},若A∩B={1},则b的值为( )| A. | -3 | B. | 3 | C. | 1 | D. | -1 |
分析 利用两个集合的交集的定义求得a 的值和 b 的值,
解答 解:∵集合A={3,log2(a-2)},B={a,a+b},A∩B={1},
∴log2(a-2)=1,∴a=4,
∴a+b=1,
∴b=-3,
故选:A.
点评 本题考查集合的表示方法、两个集合的并集的定义和求法,属于基础题.

练习册系列答案
相关题目
13.某校高二文科100名学生参加了语数英学科竞赛,年级为了解这些学生语文和数学成绩的情况,将100名学生的语文和数学成绩统计如表:
(I)若数学成绩的优秀率为35%,现利用随机抽样从数学成绩“优秀”的学生中抽取1名学生,求该生语文成绩为“及格”的概率;
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
| 语文 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 13 | m | 5 |
| 良 | 12 | n | 9 | |
| 及格 | 10 | 14 | 7 | |
(II)在语文成绩为“良”的学生中,已知m≥10,n≥10,求数学成绩“优”比“良”的人数少的概率.
8.已知$sin({α-\frac{π}{3}})=\frac{{\sqrt{3}}}{3}$,则cos$({2α+\frac{π}{3}})$=( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{7}$ | D. | $\frac{3}{7}$ |
12.若复数z满足iz=1+i,则z的共轭复数$\overline{z}$在复平面内所对应点的坐标为( )
| A. | (1,1) | B. | (1,-1) | C. | (-1,1) | D. | (-1,-1) |
13.下列命题为真命题的是( )
| A. | ?x0∈R,使得x02-x0+2=0 | |
| B. | 命题“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 在△ABC中,“A=B”是“sinA=sinB”的充要条件 |
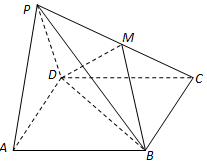 如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,面PAD⊥底面ABCD,且△PAD是边长为2的等边三角形,PC=$\sqrt{13}$,M在PC上,且PA∥面BDM.