题目内容
10.设函数f(x)=$\left\{\begin{array}{l}{2x+1,x≤0}\\{{e}^{x},x>0}\end{array}\right.$,则满足f(f(m))>f(m)+1的m的取值范围是( )| A. | $({-\frac{1}{2},+∞})$ | B. | )(0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
分析 由已知分m≤0和m>0分别求出f(m),进一步得到f(f(m)),代入f(f(m))>f(m)+1,由导数可得:当x>0时,ex>x+1,结合该式即可求得满足f(f(m))>f(m)+1的m的取值范围.
解答 解:当m≤0时,f(m)=2m+1∈(-∞,1],
若2m+1≤0,即m$≤-\frac{1}{2}$,则f(f(m))>f(m)+1?2(2m+1)+1>2m+1+1,即m>-$\frac{1}{2}$(舍);
若2m+1>0,即m$>-\frac{1}{2}$,则f(f(m))>f(m)+1?e2m+1>2m+1+1,
令g(x)=ex-x-1,g′(x)=ex-1,当x>0时,g′(x)>0,g(x)为增函数,则g(x)>g(0)=0,
∴当x>0时,ex>x+1,故e2m+1>2m+1+1成立,∴-$\frac{1}{2}<m≤0$;
当m>0时,f(m)=em>0,则f(f(m))>f(m)+1?${e}^{{e}^{m}}$>em+1,
令t=em(t>1),则et>t+1,
∵当x>0时,ex>x+1成立,∴et>t+1恒成立,则m>0时不等式f(f(m))>f(m)+1成立.
综上,满足f(f(m))>f(m)+1的m的取值范围是(-$\frac{1}{2}$,+∞).
故选:A.
点评 本题考查利用导数研究函数的单调性,考查数学转化思想方法,训练了恒成立问题的求解方法,是中档题.

练习册系列答案
相关题目
5.给定两个命题p,q,“¬(p∨q)为假”是“p∧q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.若复数z1,z2在复平面内对应的点关于x轴对称,且z1=1+2i,则$\frac{z_1}{z_2}$=( )
| A. | $-\frac{4}{5}+\frac{3}{5}i$ | B. | $-\frac{3}{5}+\frac{4}{5}i$ | C. | $-\frac{1}{2}+\frac{3}{2}i$ | D. | $-\frac{1}{2}-\frac{3}{2}i$ |
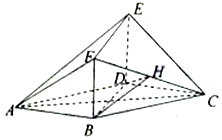 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.