题目内容
8.已知抛物线y2=2px(p>0)上一 点M(1,y0)到其焦点的距离为5,双曲线$C:{x^2}-\frac{y^2}{b^2}=1$(b>0)的左顶点为A,若双曲线C的一条渐近线垂直于直线AM,则其离心率为$\frac{{\sqrt{5}}}{2}$.分析 利用抛物线的焦点弦公式求得p的值,代入抛物线方程求得M点坐标,利用直线的斜率公式,即可求得AM的斜率,由双曲线的渐近线方程y=±bx,-b×2=-1,即可求得b的值,即可求得双曲线的离心率.
解答 解:由抛物线的定义可知:M(1,y0)到其焦点的距离为5,即1+$\frac{p}{2}$=5,
则p=8,
抛物线的标准方程y2=16x,则M(1,4)或M(1,-4),
假设M(1,4),A(-1,0),则AM的斜率为k=$\frac{4-0}{1-(-1)}$=2,
双曲线的渐近线方程y=±bx,
由双曲线C的一条渐近线垂直于直线AM,则-b×2=-1,
故b=$\frac{1}{2}$.则c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{1+\frac{1}{4}}$=$\frac{\sqrt{5}}{2}$,
双曲线的离心率e=$\frac{c}{a}$=$\frac{\sqrt{5}}{2}$,
故答案为:$\frac{\sqrt{5}}{2}$.
点评 本题考查抛物线的定义,双曲线的简单几何性质,直线的斜率公式,考查计算能力,属于中档题.

练习册系列答案
相关题目
3.△ABC内角A,B,C所对的边分别是a,b,c,则“acosA=bcosB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
13.下列命题为真命题的是( )
| A. | ?x0∈R,使得x02-x0+2=0 | |
| B. | 命题“?x∈R,x2+x+1>0”的否定是“?x0∈R,x02+x0+1<0” | |
| C. | ?θ∈R,函数f(x)=sin(2x+θ)都不是偶函数 | |
| D. | 在△ABC中,“A=B”是“sinA=sinB”的充要条件 |
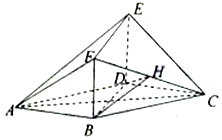 如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.
如图,在多面体ABCDEF中,平面BDEF⊥平面ABCD,四边形ABCD是菱形,四边形BDEF是矩形,BD=2BF,H是CF的中点.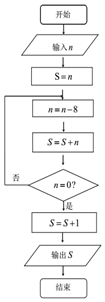 《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.
《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷.卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决此问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数n是8的整数倍时,均可采用此方法求解.如图,是解决这类问题的程序框图,若输入n=40,则输出的结果为121.