题目内容
已知点A（2，0），B(-1，
)是圆x2+y2=4上的定点，经过点B的直线与该圆交于另一点C，当△ABC面积最大时，直线BC的方程为 ．
| 3 |
考点：圆的参数方程,直线与圆的位置关系
专题：直线与圆
分析：由题意，当△ABC面积最大时，C到AB的距离最大，设C的坐标，求出直线AB的方程，可得C到AB的距离，利用三角函数的值域即可得出结论．
解答：
解：由题意，当△ABC面积最大时，C到AB的距离最大，设C（2cosα，2sinα），则
∵点A（2，0），B(-1，
)，
∴直线AB的方程为x-
y-2=0，
∴C到AB的距离为
=|2cos（α+
）-1|，
∴cos（α+
）=-1时，C到AB的距离最大为3，此时α可取
，
∴C（-1，-
），
∵B(-1，
)，直线BC的方程为x=-1．
故答案为：x=-1．
∵点A（2，0），B(-1，
| 3 |
∴直线AB的方程为x-
| 3 |
∴C到AB的距离为
|2cosα-2
| ||
|
| π |
| 3 |
∴cos（α+
| π |
| 3 |
| 2π |
| 3 |
∴C（-1，-
| 3 |
∵B(-1，
| 3 |
故答案为：x=-1．
点评：本题考查直线与圆的位置关系，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是（ ）
| A、m∥α，n∥α，则m∥n |
| B、m∥n，m∥α，则n∥α |
| C、m⊥α，m⊥β，则α∥β |
| D、α⊥γ，β⊥γ，则α∥β |
甲、乙两人同时从图书馆走向教室，甲一半路程步行，一半路程跑步；乙一半时间步行，一半时间跑步，若两人步行、跑步的速度一样，则先到教室的是（ ）
| A、甲 | B、乙 |
| C、甲、乙同时到达 | D、无法确定 |
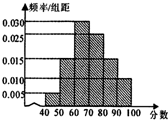某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分为6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图，已知高一年级共有学生600名，据此估计，该模块测试成绩不少于60分的学生人数为已知实数r是常数，如果M（x0，y0）是圆x2+y2=r2外的一点，那么直线x0x+y0y=r2与圆x2+y2=r2的位置关系是（ ）
| A、相交 | B、相切 |
| C、相离 | D、都有可能 |