题目内容
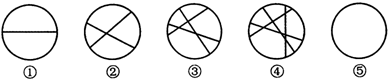
如图,在圆内画1条线段,将圆分成两部分;画2条相交线段,将圆分割成4部分;画3条线段,将圆最多分割成7部分;画4条线段,将圆最多分割成11部分,那么,
(I)在圆内画5条线段,将圆最多分割成 部分;
(Ⅱ)在圆内画n条线段,将圆最多分割成 部分.
(I)在圆内画5条线段,将圆最多分割成
(Ⅱ)在圆内画n条线段,将圆最多分割成

考点:归纳推理
专题:规律型
分析:根据1条、2条、3条、4条的特殊情况,可以发现规律,得出关系式,即可得到结论.
解答:
解答:解:(I)一条直线可以把平面分成两部分,两条直线最多可以把平面分成4部分,三条直线最多可以把平面分成7部分,四条直线最多可以把平面分成11部分,
可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
∴在圆内画5条线段,将圆最多分割成11+5=16.
(Ⅱ)由(I)知,
n=1,a1=1+1
n=2,a2=a1+2
n=3,a3=a2+3
n=4,a4=a3+4
…
n=n,an=an-1+n
以上式子相加整理得,an=1+1+2+3+…+n=1+
.
故答案为:16,1+
.
可以发现,两条直线时多了2部分,三条直线比原来多了3部分,四条直线时比原来多了4部分,…,n条时比原来多了n部分.
∴在圆内画5条线段,将圆最多分割成11+5=16.
(Ⅱ)由(I)知,
n=1,a1=1+1
n=2,a2=a1+2
n=3,a3=a2+3
n=4,a4=a3+4
…
n=n,an=an-1+n
以上式子相加整理得,an=1+1+2+3+…+n=1+
| n(n+1) |
| 2 |
故答案为:16,1+
| n(n+1) |
| 2 |
点评:本题主要考查归纳推理的应用,正确读懂题意是解决本题的关键.

练习册系列答案
相关题目
若在区间[0,2]中随机地取两个数,则这两个数中较大的数大于
的概率是( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设y=f(x)是R上的任意函数,下列叙述正确的是( )
| A、y=f(x)•f(-x)是奇函数 |
| B、y=f(x)•|f(-x)|是奇函数 |
| C、y=f(x)+f(-x)是偶函数 |
| D、y=f(x)-f(-x)是偶函数 |
 如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面A1B1C1,底面为直角三角形,∠ACB=90°,AC=2,BC=1,CC1=