题目内容
若方程
+
=1表示准线平行于x轴的椭圆,则m的范围是( )
| x2 |
| m2 |
| y2 |
| (m-1)2 |
A、m>
| ||
B、m<
| ||
C、m>
| ||
D、m<
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:根据椭圆的准线、交点与方程的关系可得椭圆的交点在y轴上,进而得到0<m2<(m-1)2,解出即可.
解答:
解:解:因为方程
+
=1表示准线平行于x轴的椭圆,
所以椭圆的交点在y轴上,
所以0<m2<(m-1)2,解得m<
且m≠0.
故选D.
| x2 |
| m2 |
| y2 |
| (m-1)2 |
所以椭圆的交点在y轴上,
所以0<m2<(m-1)2,解得m<
| 1 |
| 2 |
故选D.
点评:解决此类问题的关键是熟练掌握椭圆的有关性质,比如焦点和准线,利用性质解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x)=ax2+b(a≠0),若∫
f(x)dx=2f(x0),x0>0,则x0=( )
2 0 |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
设
,
是夹角为
的单位向量,且
=2
+3
,
=k
-4
.若
⊥
,则实数k的值为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
若cosα-3sinα=
,则tanα=( )
| 10 |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
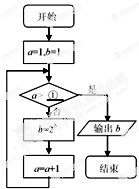 已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )
已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )