题目内容
已知a>0,且a≠1,则函数f(x)=ax+(x-1)2-2a的零点个数为( )
| A、1 | B、2 | C、3 | D、与a有关 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:令g(x)=ax-2a,h(x)=-(x-1)2,而x=1时:g(x)=ax-2a=-a<0,h(x)=-(x-1)2=0,从而得出函数有2个交点,即函数f(x)有2个零点.
解答:
解:令f(x)=0,
得:ax-2a=-(x-1)2,
令g(x)=ax-2a,h(x)=-(x-1)2,
x=1时:ax-2a=-a<0,-(x-1)2=0,
a>1时,画出函数g(x)和h(x)的草图,
如图示:
 ,
,
两个函数有2个交点;
0<a<1时,画出函数g(x)和h(x)的草图,
如图示:
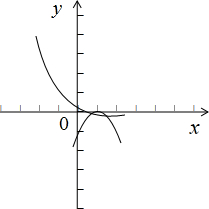 ,
,
两个函数有2个交点,
故选:B.
得:ax-2a=-(x-1)2,
令g(x)=ax-2a,h(x)=-(x-1)2,
x=1时:ax-2a=-a<0,-(x-1)2=0,
a>1时,画出函数g(x)和h(x)的草图,
如图示:
 ,
,两个函数有2个交点;
0<a<1时,画出函数g(x)和h(x)的草图,
如图示:
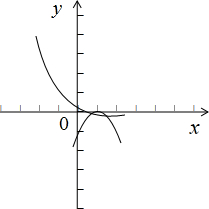 ,
,两个函数有2个交点,
故选:B.
点评:本题考查了函数的零点问题,考查转化思想,考查数形结合思想,是一道基础题.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
设
,
是夹角为
的单位向量,且
=2
+3
,
=k
-4
.若
⊥
,则实数k的值为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| a |
| b |
A、
| ||
B、
| ||
| C、16 | ||
| D、32 |
函数f(x)=|sinx|+
sinx(0≤x≤2π)与函数g(x)=a(a是常数)有两个不同的交点,则a的取值范围是( )
| 1 |
| 2 |
A、(0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
若cosα-3sinα=
,则tanα=( )
| 10 |
| A、3 | ||
B、-
| ||
| C、-3 | ||
D、
|
在△AB中,已知
•
=
•
,若|
+
|=2,且B∈[
,
],则
•
的取值范围为( )
| BC |
| CA |
| CA |
| AB |
| BA |
| BC |
| π |
| 3 |
| 2π |
| 3 |
| BA |
| BC |
A、[-2,
| ||
B、[-1,
| ||
C、[0,
| ||
D、[1,
|
对于下列表格所示五个散点,已知求得的线性回归直线方程为
=0.8x-155,则实数m的值为( )
 |
| y |
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A、8 | B、8.2 |
| C、8.4 | D、8.5 |
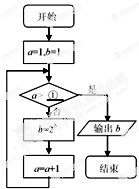 已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )
已知流程图如图(a=1,b=1下分别是a>①,b=2b,a=+1)所示,该程序运行后,为使输出的b值为16,则循环体的判断框内①处应填的是( )