题目内容
已知曲线C的方程为:x2+y2-2|x|-2|y|=0,P1、P2是曲线C上的两个点,则|P1P2|的最大值为 .
考点:曲线与方程,两点间的距离公式
专题:计算题,直线与圆
分析:利用绝对值的几何意义可知曲线C的图形,进而可得|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长.
解答:
解:利用绝对值的几何意义可知曲线C表示x2+y2-2x-2y=0,x2+y2+2x|-2y=0,x2+y2+2x+2y=0,x2+y2-2x+2y=0,分别在各个象限的部分(包括与坐标轴的交点)
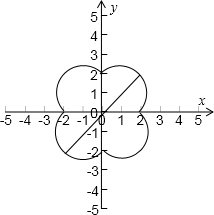
∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2
+
+
=4
.
故答案为:4
.

∵P1、P2是曲线C上的两个点,
∴|P1P2|的最大值为一、三(或二、四)象限的圆的圆心距加上2个半径的长
∴|P1P2|的最大值为2
| 2 |
| 2 |
| 2 |
| 2 |
故答案为:4
| 2 |
点评:本题考查圆的方程,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
α∈(π,
),cosα=-
则sin2α=( )
| 3π |
| 2 |
| ||
| 5 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
若角A,B分别为△ABC的内角,且B为锐角,满足sin(
-A)>sinB,则△ABC是( )
| π |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、以上情况都有可能 |
 如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2
如图,四棱锥E-ABCD,已知四边形ABCD为菱形,△AEC所在的平面垂直于平面ABCD,且∠EAC=∠BAD=60°,AD=2