题目内容
求函数y=log
(x2-4x)的单调区间和值域.
| 1 |
| 2 |
考点:复合函数的单调性
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:求出函数的定义域,令t=x2-4x,则y=log
t,由复合函数的单调性:同增异减,结合二次函数和对数函数的单调性和值域,即可得到.
| 1 |
| 2 |
解答:
解:令t=x2-4x,由t>0得x>4或x<0,
则y=log
t,即有y在t>0上递减,
由t在x>4上递增,在x<0上递减,
由复合函数的单调性:同增异减,可得,
函数y=log
(x2-4x)的单调增区间为(-∞,0),单调减区间为(4,+∞).
由于t=x2-4x=(x-2)2-4<0,
则函数y=log
(x2-4x)的值域为R.
则y=log
| 1 |
| 2 |
由t在x>4上递增,在x<0上递减,
由复合函数的单调性:同增异减,可得,
函数y=log
| 1 |
| 2 |
由于t=x2-4x=(x-2)2-4<0,
则函数y=log
| 1 |
| 2 |
点评:本题考查复合函数的单调性和值域问题,考查对数函数和二次函数的单调性和值域问题,考查运算能力,属于中档题和易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
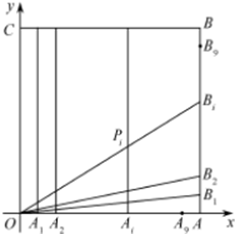 如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).
如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).