题目内容
对于任意实数x1,x2,max{x1,x2}表示x1,x2中较大的那个数,则当x∈R时,函数f(x)=max{2-x2,x},x∈[-3,
]的最大值与最小值的差是 .
| 1 |
| 2 |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:根据新定义,式子max{x1,x2}表示x1,x2中较大的那个数,则max{2-x2,x}表示2-x2,x中较大的,故可在同一坐标系内化函数y=2-x2与函数y=x的图象:两部分图象上方的部分即为函数f(x)的图象,根据图象的最高点与最低点的坐标即可求出答案.
解答:
解:∵对于实数x1,x2,式子max{x1,x2}表示x1,x2中较大的那个数,则max{2-x2,x}表示2-x2,x中较大的,
∵x∈[-3,
],
在同一坐标系内化函数y=2-x2与函数y=x的图象:两部分图象上方的部分即为函数f(x)的图象:
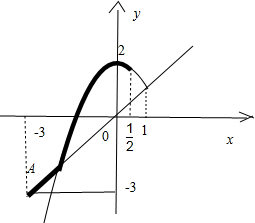
从图象上看:图象最高点的纵坐标为2,最低点的纵坐标为-3,
函数f(x)=max{2-x2,x},x∈[-3,
]的最大值与最小值的差是2-(-3)=5
故答案为:5.
∵x∈[-3,
| 1 |
| 2 |
在同一坐标系内化函数y=2-x2与函数y=x的图象:两部分图象上方的部分即为函数f(x)的图象:

从图象上看:图象最高点的纵坐标为2,最低点的纵坐标为-3,
函数f(x)=max{2-x2,x},x∈[-3,
| 1 |
| 2 |
故答案为:5.
点评:本题是一道新定义题,考查了函数的最值及其几何意义,画图解决直观形象.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把一根长度为5的铁丝截成任意长的3段,则能构成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
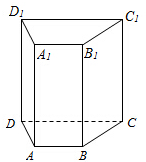 如图,直四棱柱ABCD-A1B1C1D1,底面ABCD为梯形AB∥CD,ABC=90°,BC=CD=2AB=2.
如图,直四棱柱ABCD-A1B1C1D1,底面ABCD为梯形AB∥CD,ABC=90°,BC=CD=2AB=2.