Question

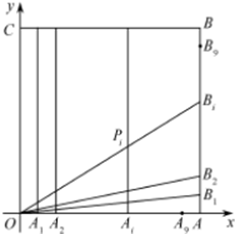如图，在正方形OABC中，O为坐标原点，点A的坐标为（10，0），点C的坐标为（0，10），分别将线段OA和AB十等分，分点分别记为A₁，A₂，…，A₉和B₁，B₂，…，B₉，连接OB_i，过A_i作x轴的垂线与OB_i，交于点P_i（i∈N*，1≤i≤9）．
（1）求证：点P_i（i∈N^*，1≤i≤9）都在同一条抛物线上，并求抛物线E的方程．
（2）过点C作直线与抛物线E交于不同的两点MN，若

MC

=

CN

，求直线的方程．

Answer 1

考点：直线与圆锥曲线的关系,抛物线的标准方程

专题：圆锥曲线中的最值与范围问题

分析：（1）由题意，求出过A_i（i∈N^*，1≤i≤9）且与x轴垂直的直线方程为x=i，B_i的坐标为（10，i），即可得到直线OB_i的方程为y=

i

10

x．由

x=i y= i 10 x

，即可得到P_i满足的抛物线方程．
（2）由题意，设直线l的方程为y=kx+10，与抛物线的方程联立得到一元二次方程，利用根与系数的关系，及利用面积公式S_△OCM=S_△OCN，可得|x₁|=4|x₂|．即x₁=-4x₂．联立即可得到k，进而得到直线方程．

解答： （1）证明：由题意，过A_i（i∈N^*，1≤i≤9）且与x轴垂直的直线方程为x=i，
B_i的坐标为（10，i），
∴直线OB_i的方程为y=

i

10

x．
设P_i（x，y），由

x=i y= i 10 x

，解得y=

x2

10

，即x²=10y．
∴点P_i（i∈N^*，1≤i≤9）都在同一条抛物线上，
抛物线E的方程为x²=10y．
（2）解：由题意，设直线l的方程为y=kx+10，
联立

y=kx+10 x2=10y

，消去y得到x²-10kx-100=0，
此时△＞0，直线与抛物线恒有两个不同的交点，
设为M（x₁，y₁），N（x₂，y₂），
则x₁+x₂=10k，x₁x₂=-100，
∵S_△OCM=4S_△OCN，∴|x₁|=4|x₂|．∴x₁=-4x₂．
联立

x1+x2=10k x1x2=-100 x1=-4x2

，解得k=±

3

2

．
∴直线l的方程为y=±

3

2

x+10．
即为3x+2y-20=0或3x-2y+20=0．

点评：本题主要考查了抛物线的性质、直线与抛物线的位置关系、三角形的面积等基础知识，考查了推理能力、转化与化归方法、计算能力、数形结合的思想方法、函数与方程思想方法、分析问题和解决问题的能力．