题目内容
19．已知命题p：?n∈N，n2＜2n，则￢p为?n0∈N，n02≥${2}^{{n}_{0}}$．分析 根据全称命题的否定是特称命题，即可得到结论．
解答 解：∵命题p是全称命题，
∴根据全称命题的否定是特称命题，可知：
￢p：?n0∈N，n02≥${2}^{{n}_{0}}$，
故答案为：?n0∈N，n02≥${2}^{{n}_{0}}$
点评 本题主要考查含有量词的命题的否定，全称命题的否定是特称命题，比较基础．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
9．将函数f（x）=2$\sqrt{3}$cos2x-2sinxcosx-$\sqrt{3}$的图象向左平移t（t＞0）个单位，所得图象对应的函数为奇函数，则t的最小值为（ ）
| A． | $\frac{2π}{3}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{2}$ | D． | $\frac{π}{6}$ |
10．执行如图所示的程序框图，输出的x值为（ ）
| A． | 0 | B． | 3 | C． | 6 | D． | 8 |
7．已知函数f（x）在（-1，+∞）上单调，且函数y=f（x-2）的图象关于x=1对称，若数列{an}是公差不为0的等差数列，且f（a50）=f（a51），则{an}的前100项的和为（ ）
| A． | -200 | B． | -100 | C． | 0 | D． | -50 |
14．下列说法错误的是（ ）
| A． | 回归直线过样本点的中心（$\overline{x}$，$\overline{y}$） | |
| B． | 两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于1 | |
| C． | 在回归直线方程$\stackrel{∧}{y}$=0.2x+0.8中，当解释变量x每增加1个单位时，预报变量$\stackrel{∧}{y}$平均增加0.2个单位 | |
| D． | 对分类变量X与Y，随机变量K2的观测值k越大，则判断“X与Y有关系”的把握程度越小 |
4．已知不等式组$\left\{\begin{array}{l}{x+y-3≥0，}&{\;}\\{x-2y+3≥0，}&{\;}\\{x≤a}&{\;}\end{array}\right.$，（a＞1）表示的平面区域为D，点（x0，y0）在平面区域D上，则3x0-y0的最小值等于（ ）
| A． | 4a-3 | B． | -1 | C． | 1 | D． | $\frac{5a-3}{2}$ |
11．已知sinα=-$\frac{12}{13}$，且α是第三象限的角，则tanα的值为（ ）
| A． | $\frac{12}{5}$ | B． | -$\frac{12}{5}$ | C． | $\frac{5}{12}$ | D． | -$\frac{5}{12}$ |
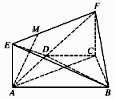如图，在梯形ABCD中，AB∥CD，AD=CD=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形，AE=a，点M在线段EF上，且MF=2EM．