题目内容
4.已知不等式组$\left\{\begin{array}{l}{x+y-3≥0,}&{\;}\\{x-2y+3≥0,}&{\;}\\{x≤a}&{\;}\end{array}\right.$,(a>1)表示的平面区域为D,点(x0,y0)在平面区域D上,则3x0-y0的最小值等于( )| A. | 4a-3 | B. | -1 | C. | 1 | D. | $\frac{5a-3}{2}$ |
分析 作出不等式组对应的平面区域,要使平面区域内存在点P(x0,y0)满足3x0-y0的最优解,求解最小值.
解答  解:作出不等式组$\left\{\begin{array}{l}{x+y-3≥0,}&{\;}\\{x-2y+3≥0,}&{\;}\\{x≤a}&{\;}\end{array}\right.$(a>1)对应的平面如图:由$\left\{\begin{array}{l}{x+y-3=0}\\{x-2y+3=0}\end{array}\right.$
解:作出不等式组$\left\{\begin{array}{l}{x+y-3≥0,}&{\;}\\{x-2y+3≥0,}&{\;}\\{x≤a}&{\;}\end{array}\right.$(a>1)对应的平面如图:由$\left\{\begin{array}{l}{x+y-3=0}\\{x-2y+3=0}\end{array}\right.$
解得交点A的坐标为(1,2),点(x0,y0)在平面区域D上,则3x0-y0的最小值就是直线3x-y=z经过点A(1,2)取得,
故3x0-y0的最小值为3-2=1.
故选:C.
点评 本题主要考查线性规划的基本应用,利用数形结合是解决本题的关键,综合性较强.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
12.已知集合A={x|0≤x≤5},B={x∈N*|x-1≤2}则A∩B=( )
| A. | {x|1≤x≤3} | B. | {x|0≤x≤3} | C. | {1,2,3} | D. | {0,1,2,3} |
13.如图,P为正方体ABCD-A1B1C1D1中AC1与BD1的交点,则△PAC在该正方体各个面上的射影可能是( )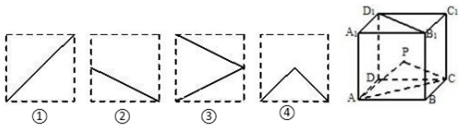

| A. | ①②③④ | B. | ①③ | C. | ①④ | D. | ②④ |