题目内容

已知x∈R，f（x）表示x+1，
x
2
，3-2x中最小的一个，求函数f（x）的解析式和最大值．
考点：函数的最值及其几何意义,函数解析式的求解及常用方法
专题：计算题,数形结合
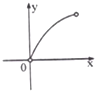
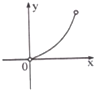
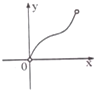
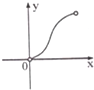
分析：先分别画出x+1，
x
2
，3-2x的图象，然后取最小的那段，从而可得函数（x）的解析式，结合图象可得最大值．
解答： 解：

f（x）=
x+1，x＜-2
x
2
，-2≤x≤
6
5
3-2x，x＞
6
5
，最大值为f（
6
5
）=
3
5
．
点评：本题主要考查了分段函数的图象，同时考查了分段函数的最值得求解，以及运算求解的能力．
练习册系列答案
相关题目
过椭圆
x2
2
+y2=1的一个焦点F作直线l交椭圆于点A、B两点，椭圆的中心为O，当△AOB面积最大时，求直线l的方程．
2014世界园艺博览会在青岛举行，某展销商在此期间销售一种商品，根据市场调查，当每套商品售价为x元时，销量可以达到15-0.1x万套，供货商把该产品的供货价格分为两部分，其中固定价格为每套30元，浮动价格与销量（单位：万套）成反比，比例系数为k，假设不计其它成本，即每套产品销售利润=售价-供货价格．
（1）若售价为50元时，展销商的总利润为180万元，求售价为100元时的销售总利润；
（2）若k=10，求销售这套商品总利润的函数f（x），并求f（x）的最大值．
对向量
a
=（a1，a2），
b
=（b1，b2）定义一种运算“⊕”：a?b=（a1，a2）⊕（b1，b2）=（a1b1，a2b2），已知动点P，Q分别在曲线y=sinx和y=f（x）上运动，且
OQ
=m⊕
Op
+m（其中O为坐标原点），若向量
m
=（
1
2
，3），
n
=（
π
6
，0），则y=f（x）的最大值为
 
．
已知符号函数sgn=
1(x＞0)
0(x=0)
-1(x＜1)
则函数f（x）=sgn（ln x）-ln2x的零点个数为
 
．
若奇函数f（x）在区间[2，5]上的最小值是5，那么f（-x）在区间[-5，-2]上有（　　）
A、最小值-5B、最小值5
C、最大值-5D、最大值5
已知函数f（x）=
1+x
+
1-x
．
（1）求函数f（x）的定义域并判断函数的奇偶性；
（2）设F（x）=m
1-x2
+f（x），若记f（x）=t，求函数F（x）的最大值的表达式g（m）．
正方体ABCD-A1B1C1D1中，P，Q分别是线段（不包括端点）CC1，BD上的点，PQ∥ABC1D1，记CP=x，四面体PQA1B1的体积为y，则y关于x的函数大致图象是（　　）
A、
B、
C、
D、
设f（x）是定义域为R的偶函数，且对任意实数x，恒有f（x+1）=-f（x），已知x∈（0，1）时，f（x）=log
1
2
（1-x），则函数f（x）在（1，2）上（　　）
A、是增函数，且f（x）＜0
B、是增函数，且f（x）＞0
C、是减函数，且f（x）＜0
D、是减函数，且f（x）＞0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网