题目内容
设a、b、c是三条不同直线,α,β,γ是三个不同平面,则下列命题正确题是( )
①若α⊥γ,β⊥γ,则α∥β;
②若a、b异面,a?α,b?β,a∥β,b∥α,则α∥β;
③若α∩β=a,β∩γ=b,γ∩α=c,且a∥b,则c∥β;
④若a,b为异面直线,a∥α,b∥α,c⊥a,c⊥b,则c⊥α.
①若α⊥γ,β⊥γ,则α∥β;
②若a、b异面,a?α,b?β,a∥β,b∥α,则α∥β;
③若α∩β=a,β∩γ=b,γ∩α=c,且a∥b,则c∥β;
④若a,b为异面直线,a∥α,b∥α,c⊥a,c⊥b,则c⊥α.
| A、①②④ | B、②④ |
| C、②③④ | D、③④ |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:①α与β也可能相交.②由面面平行的判定定理判断.③由线面平行的判定定理判断.④由线面垂直的判定定理判断.
解答:
解:①若α⊥γ,β⊥γ,则α与β相交或平行,故①错误;
②若a、b异面,a?α,b?β,a∥β,b∥α,
则由面面平行的判定定理知α∥β,故②正确;
③若α∩β=a,β∩γ=b,γ∩α=c,且a∥b,
则由线面平行的判定定理知c∥β,故③正确;
④若a,b为异面直线,a∥α,b∥α,c⊥a,c⊥b,
则由线面垂直的判定定理知c⊥α,故④正确.
故选:C.
②若a、b异面,a?α,b?β,a∥β,b∥α,
则由面面平行的判定定理知α∥β,故②正确;
③若α∩β=a,β∩γ=b,γ∩α=c,且a∥b,
则由线面平行的判定定理知c∥β,故③正确;
④若a,b为异面直线,a∥α,b∥α,c⊥a,c⊥b,
则由线面垂直的判定定理知c⊥α,故④正确.
故选:C.
点评:本题主要考查异面直线,线面平行,面面平行,线面垂直的判定定理,对定理的三种语言掌握要清晰,准确,灵活.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某厂去年的产值记为1,计划从今年起,每年的产值比上年增长8%,则从今年起到第十年,这个厂这十年的总产值为( )
| A、1.089 | ||
| B、1.0810 | ||
C、
| ||
D、
|
如图是某一四棱锥的三视图,则这个四棱锥的体积为( )


| A、4 | B、8 | C、16 | D、20 |
已知随机变量X服从正态分布N(1,4),且P(0≤X≤2)=0.68,则P(X>2)=( )
| A、0.34 | B、0.16 |
| C、0.84 | D、0.32 |
函数f(x)=
的值域是( )
| 1-x2012 |
| 1+x2012 |
| A、[-1,1] |
| B、(-1,1] |
| C、[-1,1) |
| D、(-1,1) |
定义在R上的函数f(x)不是常数函数,且满足对任意的x有f(x-1)=f(x+1),f(2-x)=f(x),下列5个结论:
①f(x)是单调函数,
②f(x)的图象关于x=1对称,
③f(x)是周期函数,
④f(x)是偶函数,
⑤f(x)有最大值和最小值.
其中真命题是( )
①f(x)是单调函数,
②f(x)的图象关于x=1对称,
③f(x)是周期函数,
④f(x)是偶函数,
⑤f(x)有最大值和最小值.
其中真命题是( )
| A、②③④ | B、②③⑤ |
| C、①②⑤ | D、①②③ |
已知函数f(x)是R上的奇函数,且在R上有f′(x)>0,则f(1)的值 ( )
| A、恒为正数 | B、恒为负数 |
| C、恒为0 | D、可正可负 |
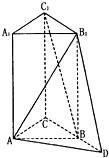 已知正三棱柱ABC-A1B1C1中,AA1=2AC=4,延长CB至D,使CB=BD.
已知正三棱柱ABC-A1B1C1中,AA1=2AC=4,延长CB至D,使CB=BD.