题目内容

13．在直角坐标系xOy中，设集合Ω={（x，y）|0≤x≤2，0≤y≤1}，在区域Ω内任取一点P（x，y），则满足x+y≥1的概率是$\frac{3}{4}$．

分析 画出满足条件的平面区域，求出阴影部分的面积，从而求出满足条件的概率即可．

解答 解：画出满足条件$\left\{\begin{array}{l}{0≤x≤2}\\{0≤y≤1}\\{x+y≥1}\end{array}\right.$的平面区域，如图示：
，
四边形OABC的面积是2，
四边形ABCD的面积是2-$\frac{1}{2}$=$\frac{3}{2}$，
故P=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$，
故答案为：$\frac{3}{4}$．

点评 本题考查了几何概型问题，考查数形结合思想，是一道基础题．

练习册系列答案
相关题目
3．已知函数f（x）=ex-x+$\frac{1}{2}{x^2}（e$为自然对数的底数）g（x）=$\frac{1}{2}{x^2}$+ax+b（a∈R，b∈R）．
（Ⅰ）求f（x）的极值；
（Ⅱ）若f（x）≥g（x），求b（a+1）的最大值．
4．中国古代数学名著《算法统宗》中，许多数学问题都是以诗歌的形式呈现，其中一首诗可改编如下：“甲乙丙丁戊，酒钱欠千文，甲兄告乙弟，三百我还与，转差十几文，各人出怎取？”意为：五兄弟，酒钱欠千文，甲还三百，甲乙丙丁戊还钱数依次成等差数列，在这个问题中丁该还150文钱．
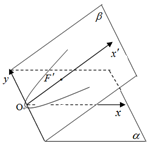1．具有公共y轴的两个直角坐标平面α和β所成的二面角α-y轴-β等于60°，已知β内的曲线C'的方程是y2=4x'，曲线C'在α内的射影在平面α内的曲线方程为y2=2px，则p=1．
8．已知抛物线C的焦点坐标在x轴上且开口向右，焦点与准线的距离为4，定点M（-2，2），过C的焦点且斜率为k的直线与C交于A，B两点，
（1）抛物线C的标准方程；
（2）若$\overrightarrow{MA}$•$\overrightarrow{MB}$=0，求直线的方程．
18．如图，在三棱锥S-ABC中，△ABC为直角三角形，且∠ACB=90°，SA⊥平面ABC，AD⊥SC．
求证：AD⊥平面SBC．
5．已知条件p：2k-1≤x≤-3k，条件q：-1＜x≤3，且p是q的必要条件，则实数k的取值范围是k≤-1．
2．已知函数f（x）=（$\frac{1}{2}$）x的图象与函数y=g（x）的图象关于直线y=x对称．
（1）若f（g（x））=6-x2，求实数x的值；
（2）若函数y=g（f（x2））的定义域为[m，n]（m≥0），值域为[2m，2n]，求实数m，n的值；
（3）当x∈[-1，1]时，求函数y=[f（x）]2-2af（x）+3的最小值h（a）．
3．某班级要从4名男生，2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为（　　）
A．20B．18C．16D．14

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网