题目内容
3.某班级要从4名男生,2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方案种数为( )| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
分析 法一:用直接法,4人中至少有1名女生包括1女3男及2女2男两种情况,计算各种情况下的选派方案种数,由加法原理,计算可得答案;
法二:用排除法,首先计算从4男2女中选4人的选派方案种数,再计算4名都是男生的选派方案种数,由排除法,计算可得答案.
解答 解:法一:4人中至少有1名女生包括1女3男及2女2男两种情况,
故不同的选派方案种数为C12•C34+C22•C24=2×4+1×6=14;
法二:从4男2女中选4人共有C46种选法,4名都是男生的选法有C44种,
故至少有1名女生的选派方案种数为C46-C44=15-1=14.
故选D.
点评 本题考查简单的排列组合,如果分类讨论太复杂的题目最好用间接法即排除法,以避免直接的分类不全情况出现.

练习册系列答案
相关题目
11.曲线C1:y=sinx,曲线${C_2}:{x^2}+{(y+r-\frac{1}{2})^2}={r^2}$(r>0),它们交点的个数( )
| A. | 恒为偶数 | B. | 恒为奇数 | C. | 不超过2017 | D. | 可超过2017 |
15.下列判断中正确的是( )
| A. | $f(x)={(\sqrt{x})^2}$是偶函数 | B. | $f(x)=\frac{{{x^2}-x}}{x-1}$是奇函数 | ||
| C. | $f(x)=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函数 | D. | $f(x)=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$是奇函数 |
1.设函数f(x)=|x-3|+|x-a|,如果对任意x∈R,f(x)≥4,则a的取值范围是( )
| A. | (-∞,-7]∪[1,+∞) | B. | [-7,1] | C. | (-∞,-1]∪[7,+∞) | D. | [-1,7] |
2.已知点P(-2,3),点Q(-6,-1),则直线PQ的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
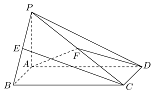 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与