题目内容
5.已知条件p:2k-1≤x≤-3k,条件q:-1<x≤3,且p是q的必要条件,则实数k的取值范围是k≤-1.分析 根据集合的包含关系得到关于k的不等式组,解出即可.
解答 解:∵p:2k-1≤x≤-3k,条件q:-1<x≤3,且p是q的必要条件,
∴(-1,3]⊆[2k-1,-3k],
∴$\left\{\begin{array}{l}{-1≥2k-1}\\{3≤-3k}\end{array}\right.$,解得:k≤-1,
故答案为:k≤-1.
点评 本题考查了充分必要条件,考查集合的包含关系,是一道基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15.已知集合A={-2,-1,0,1,2},集合B={x|x2≤1},A∩B=( )
| A. | {-2,-1,0,1} | B. | {-1,1} | C. | {-1,0} | D. | {-1,0,1} |
16.住在狗熊岭的7只动物,它们分别是熊大,熊二,吉吉,毛毛,蹦蹦,萝卜头,图图.为了更好的保护森林,它们要选出2只动物作为组长,则熊大,熊二至少一个被选为组长的概率为( )
| A. | $\frac{11}{42}$ | B. | $\frac{1}{2}$ | C. | $\frac{11}{21}$ | D. | $\frac{10}{21}$ |
15.下列判断中正确的是( )
| A. | $f(x)={(\sqrt{x})^2}$是偶函数 | B. | $f(x)=\frac{{{x^2}-x}}{x-1}$是奇函数 | ||
| C. | $f(x)=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函数 | D. | $f(x)=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$是奇函数 |
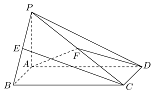 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与