题目内容
3．
如图，直三棱柱ABC-A1B1C1中，D，E分别是AB、BB1的中点，AB=BC．（1）证明：BC1∥平面A1CD；
（2）平面A1EC⊥平面ACC1A1．
分析 （1）连结AC1，交A1C点O，连DO，推出OD∥BC1，即可证明BC1∥平面A1CD．
（2）取AC的中点F，连结EO，OF，FB，证明四边形BEOF是平行四边形，证明BF⊥AC，BF⊥CC1，得到BF⊥平面ACC1A1，然后证明平面A1EC⊥平面ACC1A1．
解答 解：（1）连结AC1，交A1C点O，连DO，则O是AC1的中点，
因为D是AB的中点，故OD∥BC1…（2分）
因为OD?平面A1CD，BC1?平面A1CD…（3分）
所以BC1∥平面A1CD…（4分）
（2）取AC的中点F，连结EO，OF，FB，
因为O是AC1的中点，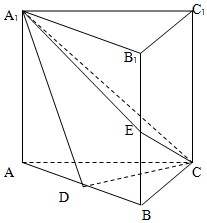
故OF∥AA1且$OF=\frac{1}{2}$AA1…（5分）
显然BE∥AA1且$BE=\frac{1}{2}$AA1
所以OF∥BE且OF=BE…（6分）
则四边形BEOF是平行四边形…（7分）
所以EO∥BF…（8分）
因为AB=BC
所以BF⊥AC…（9分）
又BF⊥CC1
所以直线BF⊥平面ACC1A1…（10分）
因为EO∥BF
所以直线EO⊥平面ACC1A1…（11分）
所以平面A1EC⊥平面ACC1A1…（12分）
点评 本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理的应用，直线与平面平行的判定定理的应用，考查逻辑推理能力．
练习册系列答案
相关题目
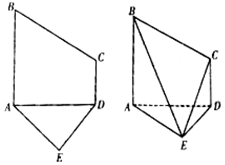已知五边形ABCDE是由直角梯形ABCD和等腰直角三角形ADE构成，如图所示，AB⊥AD，AE⊥DE，AB∥CD，且AB=2CD=2DE=4，将五边形ABCDE沿着AD折起，且使平面ABCD⊥平面ADE．
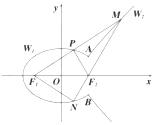如图：椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）有相同的焦点F1、F2，它们在y轴右侧有两个交点A、B，满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0．将直线AB左侧的椭圆部分（含A，B两点）记为曲线W1，直线AB右侧的双曲线部分（不含A，B两点）记为曲线W2．以F1为端点作一条射线，分别交W1于点P（xP，yP），交W2于点M（xM，yM）（点M在第一象限），设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$．