题目内容
15.过正三棱锥的侧棱与底面中心作截面,已知截面是以侧棱为底边的等腰三角形,若侧面与底面所成的角为θ,则cosθ=$\frac{1}{3}$.分析 如图,延长BO交AC于D,则D为AC中点,∠SDC为侧面和底面所成角的平面角,利用余弦定理可以求解.
解答 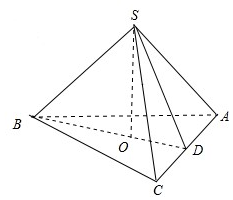 解:延长BO交AC于D,则D为AC中点.截面为△SBD.
解:延长BO交AC于D,则D为AC中点.截面为△SBD.
由正棱锥的性质,SO⊥面ABC,SD⊥AC,BD⊥AC,∠SDB为侧面和底面所成角的平面角.设底面边长BC=2.
∵SD=BD,∴SC=BC,
∵正三棱锥S-ABC为正四面体.
∴BD=$\sqrt{3}$,
在△SDB中,由余弦定理得cos∠SDB=$\frac{3+3-4}{2×\sqrt{3}×\sqrt{3}}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$
点评 本题考查线面角,考查数形结合的数学思想,考查余弦定理的运用,属于中档题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
1.若集合M={y∈N|y<6},N={x|log2(x-1)≤2},则M∩N=( )
| A. | (1,5] | B. | (-∞,5] | C. | {1,2,3,4,5} | D. | {2,3,4,5} |
10.设(1+x+x2)n=a0+a1x+…+a2nx2n,则a2+a4+…+a2n的值为( )
| A. | 3n | B. | 3n-2 | C. | $\frac{{3}^{n}-1}{2}$ | D. | $\frac{{3}^{n}+1}{2}$ |
7.设数列{an}是等差数列,Sn为其前n项和,若S5=2a5,a3=4,则a9=( )
| A. | 4 | B. | -22 | C. | 22 | D. | 80 |
4.等差数列{an}满足a1=39,a1+a3=74,则通项公式an=( )
| A. | -2n+41 | B. | -2n+39 | C. | -n2+40n | D. | -n2-40n |
5.已知函数$f(x)=sin(2x+\frac{π}{3})$,将其图象向右平移φ(φ>0)个单位后得到的函数为奇函数,则φ的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
 如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB、BB1的中点,AB=BC.