题目内容
1.在△ABC中,a,b,c分别是A,B,C的对边,a=3,c=5,B=2A,求b的值.分析 先由正弦定理得到cosA=$\frac{b}{6}$,再根据余弦定理得到b2=24,即可求出答案.
解答 解:∵a=3,c=5,B=2A,
由正弦定理得$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{b}{sin2A}$=$\frac{b}{2sinAcosA}$,
∴cosA=$\frac{b}{6}$,
由余弦定理可得,a2=b2+c2-2bccosA,
∴9=b2+25-$\frac{5}{3}$b2,
即b2=24,
∴b=2$\sqrt{6}$.
点评 本题考查了正弦定理和余弦定理,关键是能熟练应用,属于基础题.

练习册系列答案
相关题目
7.下列函数表示同一函数的是( )
| A. | f(x)=x-2和g(x)=$\frac{{x}^{2}-4}{x+2}$ | B. | f(x)=x2和g(x)=$\frac{{x}^{4}}{x}$ | ||
| C. | f(x)=$\root{3}{{x}^{3}}$和g(x)=($\sqrt{x}$)2 | D. | f(x)=4x2和g(m)=4m2 |
6.1和4的等比中项是( )
| A. | 2 | B. | ±2 | C. | $\frac{5}{2}$ | D. | 5 |
10.函数f(x)=$\frac{1}{\sqrt{2-x}}$+ln(1+x)的定义域是( )
| A. | (-2,-1) | B. | (-1,+∞) | C. | (-∞,+∞) | D. | (-1,2) |
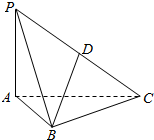 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.