题目内容
11.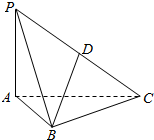 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.(1)求二面角B-PA-C的大小;
(2)求直线BD与平面ABC所成角的正切值.
分析 (1)推导出BA⊥PA,CA⊥PA,从而∠BAC为二面角B-PA-C的平面角,由此能求出二面角B-PA-C的大小.
(2)过点D作DE⊥AC,垂足为E,连接AE,直线BD与平面ABC所成的角为∠DBE,由此能求出直线BD与平面ABC所成角的正切值.
解答 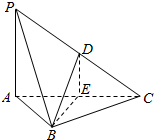 解:(1)∵PA⊥平面ABC,AC?平面ABC,AB?平面ABC,
解:(1)∵PA⊥平面ABC,AC?平面ABC,AB?平面ABC,
∴BA⊥PA,CA⊥PA,∴∠BAC为二面角B-PA-C的平面角.
在△ABC中,∵$AB=1,BC=\sqrt{3},AC=2$,
∴AB2+BC2=AC2,∴AB⊥BC,
∴△ABC为直角三角形,
sin∠BAC=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{2}$,∴∠BAC=60°,
故二面角B-PA-C的大小为60°…(5分)
(2)过点D作DE⊥AC,垂足为E,连接AE,
从而结合题意知DE⊥平面ABC,
∴直线BD与平面ABC所成的角为∠DBE,且$tan∠DBE=\frac{DE}{BE}$.
又D是PC的中点,∴$DE=\frac{1}{2}PA=\frac{{\sqrt{2}}}{2}$,$BE=\frac{1}{2}AC=1$,
∴$tan∠DBE=\frac{DE}{BE}$=$\frac{{\sqrt{2}}}{2}$.
∴直线BD与平面ABC所成角的正切值为$\frac{{\sqrt{2}}}{2}$.…(10分)
点评 本题考查三面角的大小的求法,考查线面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
3.设向量$\overrightarrow{a}$,$\overrightarrow{b}$不平行,向量$\overrightarrow{a}$+λ$\overrightarrow{b}$与3$\overrightarrow{a}$-$\overrightarrow{b}$平行,则实数λ=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{3}$ | C. | -3 | D. | -2 |
20.已知集合M={x|x+1≥0},N={x|-2<x<2},则M∩N=( )
| A. | (-∞,-1] | B. | (2,+∞) | C. | (-1,2] | D. | [-1,2) |
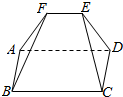 如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.
如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.