题目内容
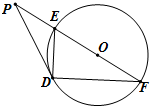 如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4
如图,P是圆O外一点,PD为切线,D为切点,割线PEF经过圆心O,若PF=12,PD=4| 3 |
考点:与圆有关的比例线段
专题:立体几何
分析:连接OD,由于PD为切线,D为切点,O为圆心,由切割线定理,求出PE,然后判断三角形的形状求出DE即可.
解答:
 (本小题满分10分)选修4-1:几何证明选讲
(本小题满分10分)选修4-1:几何证明选讲
解:连接OD,由于PD为切线,D为切点,O为圆心,所以OD⊥PD.
由切割线定理知:PD2=PE•PF,从而PE=
=4,…(5分)
所以OE=OF=OD=4,又PO=8,在Rt△PDO中,易知∠EOD=60°,故△EDO为等边三角形,所以DE=4.…(10分)
 (本小题满分10分)选修4-1:几何证明选讲
(本小题满分10分)选修4-1:几何证明选讲解:连接OD,由于PD为切线,D为切点,O为圆心,所以OD⊥PD.
由切割线定理知:PD2=PE•PF,从而PE=
| PD2 |
| PF |
所以OE=OF=OD=4,又PO=8,在Rt△PDO中,易知∠EOD=60°,故△EDO为等边三角形,所以DE=4.…(10分)
点评:本题考查切割线定理的应用,三角形的形状的判断,考查计算能力.

练习册系列答案
相关题目
在平面上,已知
⊥
,|
|=|
|=1,
=
+
,若|
|<
,则|
|的取值范围是( )
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 2 |
| OA |
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
函数f(x)=log2
是( )
| 1+x |
| 1-x |
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
 在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.
在空间四边形S-ABC中,SA=SB=SC,三角形ABC为等边三角形,M,N分别是AB,SC的中点.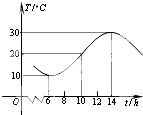 如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.