题目内容
已知两点A(-2,1),B(1,5),点C是圆x2+y2-2x+4y-4=0上的动点,则△ABC面积的最大值为( )
| A、35 | B、18 | C、16 | D、8 |
考点:点到直线的距离公式
专题:直线与圆
分析:求出圆心到直线AB的距离d,即可得出圆上的点到直线AB的最大距离为d+r,再利用三角形的面积计算公式△ABC面积的最大值=
|AB|(d+r)即可得出.
| 1 |
| 2 |
解答:
解:∵两点A(-2,1),B(1,5),
∴|AB|=
=5.
直线AB的方程为:y-5=
(x-1),即4x-3y+11=0.
圆x2+y2-2x+4y-4=0化为(x-1)2+(y+2)2=9,
可得圆心P(1,-2),半径r=3.
∴圆心P到直线AB的距离d=
=
.
∴点C到直线AB的最大距离是
+3=
.
∴△ABC面积的最大值=
|AB|(d+r)=
×
×5=18.
故选:B.
∴|AB|=
| 32+42 |
直线AB的方程为:y-5=
| 1-5 |
| -2-1 |
圆x2+y2-2x+4y-4=0化为(x-1)2+(y+2)2=9,
可得圆心P(1,-2),半径r=3.
∴圆心P到直线AB的距离d=
| |4-3×(-2)+11| |
| 5 |
| 21 |
| 5 |
∴点C到直线AB的最大距离是
| 21 |
| 5 |
| 36 |
| 5 |
∴△ABC面积的最大值=
| 1 |
| 2 |
| 1 |
| 2 |
| 36 |
| 5 |
故选:B.
点评:本题考查了圆的标准方程、点到直线的距离公式、三角形的面积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
将棱长为1的正方体木块切削成一个体积最大的球,则该球的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在同一坐标系下函数y=-x+a和y=ax图象可能是( )
A、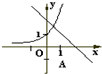 |
B、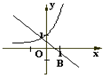 |
C、 |
D、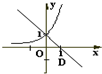 |
已知集合M={x||x+2|+|x-1|≤5},N={x|a<x<6},且M∩N=(-1,b],则b-a=( )
| A、-3 | B、3 | C、C-1 | D、7 |
已知两点A(-2,1),B(1,5),点C是圆(x-1)2+(y+2)2=9上的动点,则△ABC面积的最大值为( )
| A、36 | B、18 | C、16 | D、8 |
算法的三要素不包括以下( )
| A、明确性 | B、有限性 |
| C、有序性 | D、模糊性 |