题目内容
给出下列命题：
（1）如果λ
=λ
（λ≠0），那么
=
；
（2）若
为单位向量，
与
平行，则
=|
|•
；
（3）设
=λ1
+λ2
（λ1，λ2∈R），则当
与
共线时，
与
也共线，
其中真命题的个数是（ ）
（1）如果λ
| a |
| b |
| a |
| b |
（2）若
| a0 |
| a |
| a0 |
| a |
| a |
| a0 |
（3）设
| a |
| e1 |
| e2 |
| e1 |
| e2 |
| a |
| e1 |
其中真命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：平行向量与共线向量
专题：平面向量及应用
分析：（1）直接由向量的数乘运算判断命题正确；
（2）由向量共线的概念加以判断；
（3）零向量与任意向量共线，结合
与
共线，可判断对任意λ1，λ2∈R，有
与
也共线．
（2）由向量共线的概念加以判断；
（3）零向量与任意向量共线，结合
| e1 |
| e2 |
| a |
| e1 |
解答：
解：对于（1），由λ
=λ
（λ≠0），
两边同时乘以
，得
•λ
=
•λ
，即
=
，命题（1）正确；
对于（2），
为单位向量，
与
平行，则
=±|
|•
，命题（2）错误；
对于（3），
=λ1
+λ2
（λ1，λ2∈R），则当
与
共线时，
λ2
与λ1
共线，λ1
+λ2
与λ1
共线，则λ1
+λ2
与
共线，即
与
也共线，
命题（3）正确．
∴其中真命题的个数有2个．
故选：C．
| a |
| b |
两边同时乘以
| 1 |
| λ |
| 1 |
| λ |
| a |
| 1 |
| λ |
| b |
| a |
| b |
对于（2），
| a0 |
| a |
| a0 |
| a |
| a |
| a0 |
对于（3），
| a |
| e1 |
| e2 |
| e1 |
| e2 |
λ2
| e2 |
| e1 |
| e1 |
| e2 |
| e1 |
| e1 |
| e2 |
| e1 |
| a |
| e1 |
命题（3）正确．
∴其中真命题的个数有2个．
故选：C．
点评：本题考查平行向量与共线向量，关键是对共线向量概念的理解，是基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
设f（x）可导，且y=f（e2x），则y′=（ ）
| A、f′（e2x） |
| B、f′（e2x）e2x |
| C、2f′（e2x） |
| D、2f′（e2x）e2x |
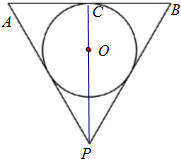设倒圆锥形容器的轴截面为一个等边三角形，在此容器内注入水，并浸入半径为r的一个实心球，使球与水面恰好相切，试求取出球后水面高为多少？