题目内容
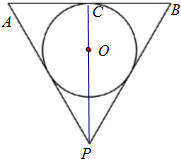设倒圆锥形容器的轴截面为一个等边三角形，在此容器内注入水，并浸入半径为r的一个实心球，使球与水面恰好相切，试求取出球后水面高为多少？考点：组合几何体的面积、体积问题
专题：计算题,空间位置关系与距离
分析：由题意求出球的体积，求出圆锥的体积，设出水的高度，求出水的圆锥的体积，利用V水+V球=V容器，求出圆锥内水平面高．
解答：
解：如图．在容器内注入水，并放入一个半径为r的铁球，这时水面记为AB，
将球从圆锥内取出后，这时水面记为EF．
三角形PAB为轴截面，是正三角形，
三角形PEF也是正三角形，圆O是正三角形PAB的内切圆．
由题意可知，DO=CO=r，AO=2r=OP，AC=
r
∴V球=
πr3，VPC=
π(
r)2•3r=3πr3
又设HP=h，则EH=
h
∴V水=
π(
h)2h=
h3
∵V水+V球=VPC
即
h3+
πr3=3πr3，
∴h=
r
即圆锥内的水深是
r．
解：如图．在容器内注入水，并放入一个半径为r的铁球，这时水面记为AB，将球从圆锥内取出后，这时水面记为EF．
三角形PAB为轴截面，是正三角形，
三角形PEF也是正三角形，圆O是正三角形PAB的内切圆．
由题意可知，DO=CO=r，AO=2r=OP，AC=
| 3 |
∴V球=
| 4 |
| 3 |
| 1 |
| 3 |
| 3 |
又设HP=h，则EH=
| ||
| 3 |
∴V水=
| 1 |
| 3 |
| ||
| 3 |
| π |
| 9 |
∵V水+V球=VPC
即
| π |
| 9 |
| 4 |
| 3 |
∴h=
| 3 | 15 |
即圆锥内的水深是
| 3 | 15 |
点评：本小题主要考查球的体积和表面积、旋转体（圆柱、圆锥、圆台）等基础知识，考查运算求解能力，考查转化思想．属于基础题．
练习册系列答案
相关题目