题目内容
已知函数f(x)=x2+2(a+1)x(x∈[-5,5]),求:
(1)当a=1时,求函数的最小值;
(2)若f(x)在(3,5)上为增函数,求a的取值范围.
(1)当a=1时,求函数的最小值;
(2)若f(x)在(3,5)上为增函数,求a的取值范围.
考点:二次函数的性质,二次函数在闭区间上的最值
专题:函数的性质及应用
分析:(1)将a=1代入,结合二次函数的图象和性质,分析函数f(x)在[-5,5]上的单调性,进而可得函数的最小值;
(2)若f(x)在(3,5)上为增函数,在区间(3,5)在函数图象对称轴的右侧,由此构造关于a的不等式,解得a的取值范围.
(2)若f(x)在(3,5)上为增函数,在区间(3,5)在函数图象对称轴的右侧,由此构造关于a的不等式,解得a的取值范围.
解答:
解:(1)当a=1时,f(x)=x2+4x的图象开口朝上,且以直线x=-2为对称轴,
故f(x)在[-5,-2]上为减函数,在[-2,5]上为增函数,
故当x=-2时,函数取最小值-4;
(2)函数f(x)=x2+2(a+1)x的图象开口朝上,且以直线x=-(a+1)为对称轴,
若f(x)在(3,5)上为增函数,
则-(a+1)≤3,
解得:a≥-4
故f(x)在[-5,-2]上为减函数,在[-2,5]上为增函数,
故当x=-2时,函数取最小值-4;
(2)函数f(x)=x2+2(a+1)x的图象开口朝上,且以直线x=-(a+1)为对称轴,
若f(x)在(3,5)上为增函数,
则-(a+1)≤3,
解得:a≥-4
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
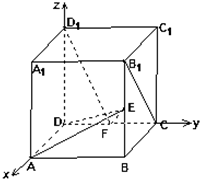 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,