题目内容
已知椭圆中心在坐标原点，焦点在x轴上，短轴端点和焦点组成边长为5的菱形，椭圆的离心率为e=
．
（1）求椭圆标准方程；
（2）设点p是椭圆上的动点，记p点到直线l：4x-5y+40=0的距离为d，求d的最大值和最小值．
| 4 |
| 5 |
（1）求椭圆标准方程；
（2）设点p是椭圆上的动点，记p点到直线l：4x-5y+40=0的距离为d，求d的最大值和最小值．
考点：直线与圆锥曲线的综合问题
专题：计算题,圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析：（1）设椭圆方程为
+
=1，运用离心率公式，菱形的边长即长半轴长，及a，b，c的关系，即可求出椭圆方程；
（2）设直线l′的方程为：4x-5y+m=0，当直线l′与椭圆相切时，d=
，由4x-5y+m=0及
+
=1，消去y，得到关于x的方程，运用判别式为0，求出m，即可得到最值．
| x2 |
| a2 |
| y2 |
| b2 |
（2）设直线l′的方程为：4x-5y+m=0，当直线l′与椭圆相切时，d=
| |m-40| | ||
|
| x2 |
| 25 |
| y2 |
| 9 |
解答：
解：（1）设椭圆方程为
+
=1，
∵a=5，
=
，b2=a2-c2，∴a=5，b=3，
故所求方程为
+
=1；
（2）设直线l′的方程为：4x-5y+m=0，
当直线l′与椭圆相切时，记切点p到l的距离为d，d=
，
由4x-5y+m=0及
+
=1，
消去y得9x2+（4x+m）2=9×25，即25x2+8mx+m2-225=0，
令△=64m2-4×25（m2-9×25）=0，则36m2=36×252，m=±25，
当m=25时 得d=
，当m=-25时 得d=
故d的最大值为d=
，d的最小值为
．
| x2 |
| a2 |
| y2 |
| b2 |
∵a=5，
| c |
| a |
| 4 |
| 5 |
故所求方程为
| x2 |
| 25 |
| y2 |
| 9 |
（2）设直线l′的方程为：4x-5y+m=0，
当直线l′与椭圆相切时，记切点p到l的距离为d，d=
| |m-40| | ||
|
由4x-5y+m=0及
| x2 |
| 25 |
| y2 |
| 9 |
消去y得9x2+（4x+m）2=9×25，即25x2+8mx+m2-225=0，
令△=64m2-4×25（m2-9×25）=0，则36m2=36×252，m=±25，
当m=25时 得d=
| 15 | ||
|
| 65 | ||
|
故d的最大值为d=
| 65 | ||
|
| 15 | ||
|
点评：本题椭圆方程和性质，主要是离心率的运用，考查直线与椭圆的位置关系，主要是相切，考查联立直线和椭圆方程，运用判别式为0，考查两平行直线的距离公式，属于中档题．
练习册系列答案
天天向上口算本系列答案
相关题目
设A（3，2，1），B（1，0，5），C（0，0，1），则AB的中点M到点C的距离为（ ）
| A、1 | B、2 | C、3 | D、4 |
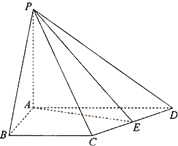如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是D的中点．证明：CD⊥平面PAE．