题目内容
在极坐标系中，以点（1，0）为圆心，1为半径的圆的极坐标方程是 ．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：以点（1，0）为圆心，1为半径的圆为（x-1）2+y2=1，把
代入即可得出．
|
解答：
解：以点（1，0）为圆心，1为半径的圆为（x-1）2+y2=1，
把
代入可得ρ2-2ρcosθ=0，即ρ=2cosθ．
故答案为：ρ=2cosθ．
把
|
故答案为：ρ=2cosθ．
点评：本题考查了直角坐标化为极坐标方程，属于基础题．
练习册系列答案
相关题目
若sin2θ=1，则tanθ+
的值是（ ）
| cosθ |
| sinθ |
| A、2 | ||
| B、-2 | ||
| C、±2 | ||
D、
|
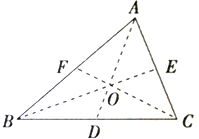如图，在△ABC中，D、E、F分别是BC、CA、AB的中点，O是三角形内一点．求证：