题目内容

1．已知数列{an}满足：2a1+22a2+23a3+…+2nan=n（n∈N*），数列{$\frac{1}{lo{g}_{2}{a}_{n}•lo{g}_{2}{a}_{n+1}}$}的前n项和为Sn，则S1•S2•S3…S10=$\frac{1}{11}$．

分析 根据2a1+22a2+23a3+…+2nan=n，求出an=$\frac{1}{{2}^{n}}$，再利用对数的运算性质和裂项法即可得到$\frac{1}{lo{g}_{2}{a}_{n}•lo{g}_{2}{a}_{n+1}}$=$\frac{1}{n}$-$\frac{1}{n+1}$，裂项求和得到Sn，代值计算即可．

解答 解：∵2a1+22a2+23a3+…+2nan=n，
∴2a1+22a2+23a3+…+2n-1an-1=n-1，
∴2nan=1，
∴an=$\frac{1}{{2}^{n}}$，
∴$\frac{1}{lo{g}_{2}{a}_{n}•lo{g}_{2}{a}_{n+1}}$=$\frac{1}{lo{g}_{2}{2}^{-n}•lo{g}_{2}{2}^{-（n+1）}}$=$\frac{1}{n（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$，
∴Sn=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$，
∴S1•S2•S3…S10=$\frac{1}{2}$×$\frac{2}{3}$×$\frac{3}{4}$×…×$\frac{9}{10}$×$\frac{10}{11}$=$\frac{1}{11}$，
故答案为：$\frac{1}{11}$

点评 本题考查了数列的通项公式的求法和裂项求和，属于中档题．

练习册系列答案
相关题目
11．若集合A={-2，-1，0，1，2}，集合B={x|lg（x+1）＞0}，则A∩B等于（　　）
A．{-1，0，1，2}B．{-1，-2}C．{1，2}D．{0，1，2}
12．某市为了制定合理的节电方案，供电局对居民用电进行了调查，通过抽样，获得了某年200户居民每户的月均用电量（单位：度），将数据按照[0，100），[100，200），[200，300），[300，400），[400，500），[500，600），[600，700），[700，800），[800，900]分成9组，制成了如图所示的频率分布直方图．
（Ⅰ）求直方图中m的值并估计居民月均用电量的中位数；
（Ⅱ）从样本里月均用电量不低于700度的用户中随机抽取4户，用X表示月均用电量不低于800度的用户数，求随机变量X的分布列及数学期望．
9．一个多面体的三视图和直观图如图所示，M是AB的中点，一只蜻蜓在几何体ADF-BCE内自由飞翔，则它飞入几何体F-AMCD内的概率为（　　）
A．$\frac{3}{4}$B．$\frac{2}{3}$C．$\frac{1}{3}$D．$\frac{1}{2}$
16．满足{1，2}⊆P?{1，2，3，4}的集合P的个数是（　　）
A．2B．3C．4D．5
6．如图，在梯形ABCD中，AB∥CD，AD=DC=CB=2，∠ABC=60°，平面ACEF⊥平面ABCD，四边形ACEF是菱形，∠CAF=60°．
（1）求证：BC⊥平面ACEF；
（2）求平面ABF与平面ADF所成锐二面角的余弦值．
13．已知Sn为数列{an}的前n项和，对n∈N*都有Sn=1-an，若bn=log2an，则$\frac{1}{{{b_1}{b_2}}}$+$\frac{1}{{{b_2}{b_3}}}$+…+$\frac{1}{{{b_n}{b_{n+1}}}}$=$\frac{n}{n+1}$．
11．已知抛物线的顶点是双曲线16x2-9y2=144的中心，而焦点是双曲线的右顶点，求抛物线的标准方程．
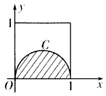12．如图正方形的曲线C是以1为直径的半圆，从区间[0，1]上取1600个随机数x1，x2，…，x800，y1，y2，…，y800，已知800个点（x1，y1），（x2，y2），…，（x800，y800）落在阴影部分阴影部分的个数为m，则m的估计值为（　　）
A．157B．314C．486D．628

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网