题目内容
3.已知数列{an}中,an2+2an-n2+2n=0(n∈N+)(Ⅰ)求数列{an}的通项公式
(Ⅱ)求数列{an}的前n项和Sn.
分析 (I)an2+2an-n2+2n=0(n∈N+),可得(an+n)(an-n+2)=0.即可解出.
(II)利用等差数列的求和公式即可得出.
解答 解:(I)∵an2+2an-n2+2n=0(n∈N+),∴(an+n)(an-n+2)=0.
∴an=-n,或an=n-2.
(II)an=-n时,Sn=-$\frac{n(n+1)}{2}$.
an=n-2时,Sn=$\frac{n(-1+n-2)}{2}$=$\frac{n(n-3)}{2}$.
点评 本题考查了一元二次方程的解法、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.已知△ABC的内角A、B、C的对边分别为a、b、c.若a=bcosC+csinB,且△ABC的面积为1+$\sqrt{2}$.则b的最小值为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
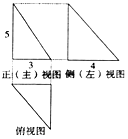
8.《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著.其中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的四面体称之为鳖膈.已知直三棱柱A1B1C1-ABC中,AB⊥BC,AB=3,$BC=4,A{A_1}=5\sqrt{3}$,将直三棱柱沿一条棱和两个面的对角线分割为一个阳马和一个鳖膈,则鳖膈的体积与其外接球的体积之比为( )
| A. | $\sqrt{3}:15π$ | B. | $3\sqrt{3}:5π$ | C. | $3\sqrt{3}:50π$ | D. | $3\sqrt{3}:25π$ |
15.在等比数列{an}中,已知a3,a7是方程x2-6x+1=0的两根,则a5=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 3 |
12.某几何体的三视图如图所示,若该几何体的体积是12π,则它的表面积是( )
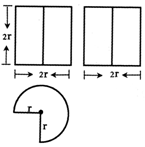

| A. | 18π+16 | B. | 20π+16 | C. | 22π+16 | D. | 24π+16 |
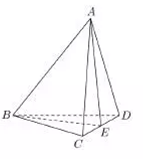 如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;
如图,三棱锥A-BCD中,△BCD为等边三角形,AC=AD,E为CD的中点;