��Ŀ����
8�����������������ҹ���ѧʷ�Ͽ���ŷ����á�����ԭ��������������ѧ���������У�������Ϊ����������һ����������洹ֱ��������֮Ϊ���������ĸ��涼Ϊֱ�������ε��������֮Ϊ��������ֱ֪������A1B1C1-ABC�У�AB��BC��AB=3��$BC=4��A{A_1}=5\sqrt{3}$����ֱ��������һ�����������ĶԽ��߷ָ�Ϊһ��������һ�������������������������������֮��Ϊ��������| A�� | $\sqrt{3}��15��$ | B�� | $3\sqrt{3}��5��$ | C�� | $3\sqrt{3}��50��$ | D�� | $3\sqrt{3}��25��$ |
���� �ֱ�������������������������������ɵó����ۣ�
��� �⣺�����⣬���������=$\frac{1}{3}��\frac{1}{2}��3��4��5\sqrt{3}$=10$\sqrt{3}$��
�������İ뾶Ϊ$\frac{1}{2}\sqrt{25+75}$=5�����Ϊ$\frac{4}{3}��•{5}^{3}$=$\frac{500}{3}��$��
�����������������������֮��Ϊ10$\sqrt{3}$��$\frac{500}{3}��$=3$\sqrt{3}$��50�У�
��ѡC��
���� ���⿼�����������������������������ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
 ��ǰ����ϵ�д�
��ǰ����ϵ�д�
�����Ŀ
16����֪������R�ϵĺ���f��x��=2|x-m|-1��m��R��Ϊż��������a=f��-2����b=f��log25����c=f��2m������a��b��c�Ĵ�С��ϵΪ��������
| A�� | a��b��c | B�� | c��a��b | C�� | a��c��b | D�� | c��b��a |
13��˫����mx2+ny2=1��mn��0����һ�������߷���Ϊ$y=\sqrt{3}x$��������������Ϊ��������
| A�� | 2 | B�� | $\frac{{2\sqrt{3}}}{3}$ | C�� | $\sqrt{3}$��$\frac{{2\sqrt{3}}}{3}$ | D�� | 2��$\frac{{2\sqrt{3}}}{3}$ |
17����֪����A={x|x��3��x��1}��B={x|x2-6x+8��0}����∁RA����B=��������
| A�� | ��1��3�� | B�� | ��1��4�� | C�� | ��2��3�� | D�� | ��2��4�� |
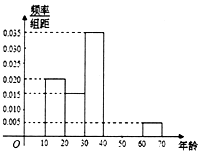 2017�������Ӿٰ��һ���Ļ����ǽ�Ŀ���й�ʫ�ʴ�ᡷ���ܹ���ϲ����ij���ߵ����˲���������[10��70]�Ĺ��ڣ��õ�����Ƶ�ʷֲ�ֱ��ͼ�������ġ��塢������������γɵȲ����У��ҵ�������4�ˣ�
2017�������Ӿٰ��һ���Ļ����ǽ�Ŀ���й�ʫ�ʴ�ᡷ���ܹ���ϲ����ij���ߵ����˲���������[10��70]�Ĺ��ڣ��õ�����Ƶ�ʷֲ�ֱ��ͼ�������ġ��塢������������γɵȲ����У��ҵ�������4�ˣ�