题目内容
已知实数a,b满足a+b=1,则(a+2)2+(b+2)2的最小值为 .
考点:圆方程的综合应用
专题:综合题,数形结合,转化思想
分析:由题意(a+2)2+(b+2)2的几何意义是点(a,b)与点(-2,-2)的距离的平方,(a+2)2+(b+2)2的最小值点(-2,-2)到直线a+b=1的距离的平方,由此问题转化为求点(-2,-2)到直线a+b=1的距离
解答:
解:由题意(a+2)2+(b+2)2的几何意义是点(a,b)与点(-2,-2)的距离的平方
实数a,b满足a+b=1,即点(a,b)在直线a+b=1运动,
∴两点(a,b)与点(-2,-2)的距离的最小值即为点(-2,-2)到直线a+b=1的距离
由于d=
=
∴(a+2)2+(b+2)2的最小值为
故答案为:
.
实数a,b满足a+b=1,即点(a,b)在直线a+b=1运动,
∴两点(a,b)与点(-2,-2)的距离的最小值即为点(-2,-2)到直线a+b=1的距离
由于d=
| |-2-2-1| | ||
|
| 5 |
| 2 |
| 2 |
∴(a+2)2+(b+2)2的最小值为
| 25 |
| 2 |
故答案为:
| 25 |
| 2 |
点评:本题考查圆的方程的应用,点到直线的距离公式,解题的关键是理解题意,将求(a+2)2+(b+2)2的最小值问题转化为点(-2,-2)到直线a+b=1的距离的平方,本题考查了转化的思想,数形结合的思想,本题考查析几何的根本问题,题目难度不大,但很有价值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
多项式1-a2-b2+2ab分解因式的结果是( )
| A、(1-a-b)(1+a+b) |
| B、(1+a-b)(1-a+b) |
| C、(a+b+1)(a-b-1) |
| D、-(a-b+1)(a+b-1) |
已知直线y=ex+1与曲线y=ex+a相切(e是自然对数的底数),则a的值是( )
| A、e | ||
B、
| ||
| C、e+1 | ||
| D、1 |
等差数列{an}的首项a1=-5,它的前11项的平均值为5,从前11项中抽去某一项后,余下的10项平均值为4,则抽去的一项是( )
| A、a5 |
| B、a6 |
| C、a10 |
| D、a11 |
 如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.
如图是某电视剧在各年龄段人群收视情况的频率分布直方图.若某村观看此电视剧的观众人数为1400人,则其中50岁以上(含50岁)的观众约有( )人.| A、504 | B、501 |
| C、500 | D、550 |
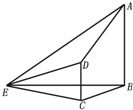 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.